Roots and Radicals
Section 10.1 Solving Quadratic Equations by the Square
Root Property
The Square root Property
Ex: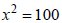
Solve:
Ex: 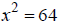
Ex: 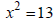
Ex: 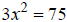
Ex: 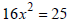
Ex: 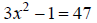
Ex: 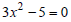
Ex: 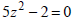
Ex: 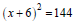
Ex: 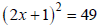
Ex: 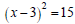
Ex: 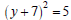
Solve each quadratic equation by first factoring the
perfect square trinomial on
the left side. Then apply the square root property. Simplify radicals, if
possible.
EX: 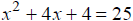
EX: 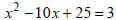
Use the Pythagorean Theorem to find the missing length in
each right triangle.
Express the answer in radical form and simplify, if possible.
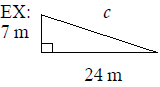
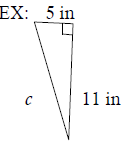
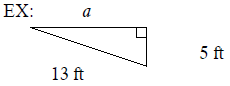
Review Exam #8
Evaluate each expression, or state that the expression is not a real number.
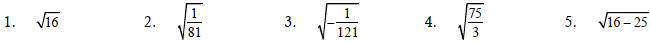
Use a calculator to approximate each expression. Round to
three decimal places. If the expression is not a real
number so that an approximation is not possible say so.

Find each cube root.

Find the indicated root, or state that the expression is
not a real number.
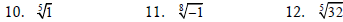
Use the product rule for square roots to find each
product.
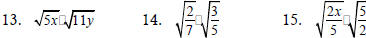
Simplify each expression. If the expression cannot be
simplified say so.
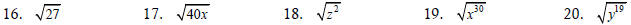
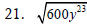
Multiply and, if possible, simplify.

Simplify using the quotient rule for square roots.
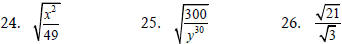
Simplify each radical expression.
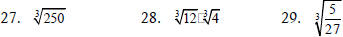
Solve the quadratic equation by the square root property.
If possible, simplify radicals or rationalize denominators.
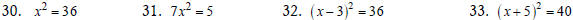
Solve the quadratic equation by first factoring the
perfect square trinomial on the left side. Then apply the square
root property. If possible, simplify radicals or rationalize denominators.

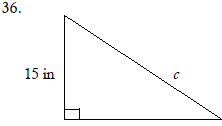
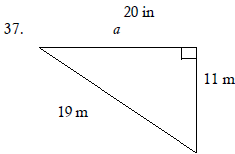
Use the Pythagorean Theorem to find the missing length in
the right triangle. Express the answer in radical form,
and simplify if possible.
Answer Key
1. 4
2. 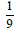
3. Not a real number.
4. 5
5. Not a real number.
6. 10.449
7. 2.646
8. -4
9. 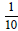
10. 1
11. Not a real number.
12. 2
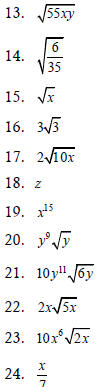
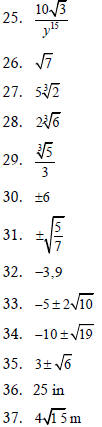
|