Solving Radical Equations
|
The Pythagorean Theorem |
|
In any right triangle, if a and b are the lengths of the legs of the
triangle and c is the length of
the hypotenuse, then we have the following |
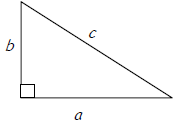 |
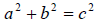
or alternately
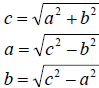 |
Other types of applications require us to interpret and
use a given formula.
Example 3:
Find the missing side of the right triangle if
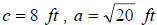 . .
Solution:
First we start by drawing the picture
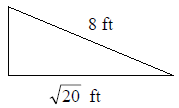
So we can see that we are clearly missing side b.
Therefore we can use the formula
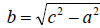 . We get . We get
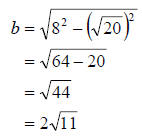
So 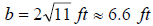 . .
Example 4:
The equation for the time of one pendulum swing (called the period of the
pendulum) is given by
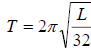 where T is the time in seconds and L is the
length in feet. Find the length of a where T is the time in seconds and L is the
length in feet. Find the length of a
pendulum of a clock that has a period of 2.3 seconds.
Solution:
We simply need to put the value of 2.3 into the formula
for T and solve for L by using the
techniques we learned in this section. We proceed as follows
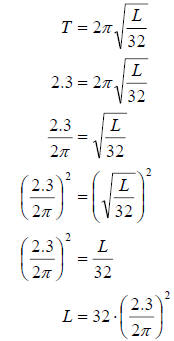
Now we put this into our calculator to get
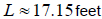 . Upon checking this value, we find that . Upon checking this value, we find that
it does check and therefore the length of the pendulum is 17.15 feet.
8.7 Exercises
Solve.
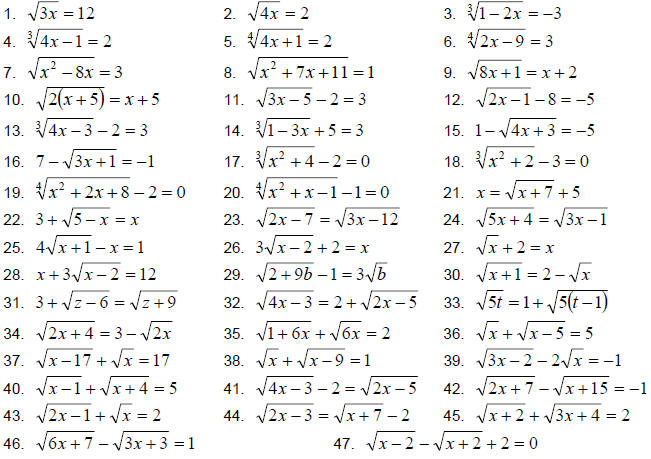

Solve for the indicated variable.
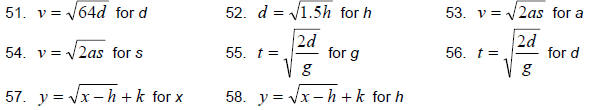
Find the missing side of the right triangle.
63. A ten foot ladder is leaning against a wall. How far
is the bottom of the ladder from the wall
when the ladder reaches a height of 8 feet?
64. A 25 foot ladder is leaning against a building. How high up the building
does the ladder
reach if the bottom of the ladder is 5 feet from the building?
65. The diagonal of a TV is 15 inches. The width of the TV is 10 inches. What is
the height of
the TV?
66. A computer monitor has a width of 13 inches and a height of 10 inches. What
is the length of
the diagonal of the monitor?
67. A stereo receiver is in a corner of a 12 foot by 14 foot room. Speaker wire
will run under a
rug, diagonally, to a speaker in the far corner. If a 4 foot slack is needed at
each end, how
long of a piece of wire should be used?
68. A baseball diamond is a square which is 90 feet on the side. What is the
distance from first base
to third base?
69. The formula for the speed of a falling object is
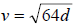 where v is the speed of the object where v is the speed of the object
in feet per second and d is the distance the object has fallen, in feet. What
distance has an
object fallen if its speed is 150 feet per second?
70. The formula for the speed of a falling object is
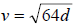 where v is the speed of the object where v is the speed of the object
in feet per second and d is the distance the object has fallen, in feet. What
distance has an
object fallen if its speed is 75 feet per second?
71. The formula for the distance a lookout can see is
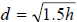 where d is the distance in where d is the distance in
miles and h is the height of the lookout above the water, in feet. How high will
the periscope
have to go to see a ship that is 6.5 miles away?
72. The formula for the distance a lookout can see is
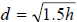 where d is the distance in where d is the distance in
miles and h is the height of the lookout above the water, in feet. How high will
the periscope
have to go to see an island that is 4.3 miles away?
73. The equation for the period of the pendulum is given
by 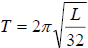 where T is the time in where T is the time in
seconds and L is the length in feet. Find the length of a pendulum of a clock
that has a
period of 4 seconds.
74. The equation for the period of the pendulum is given by
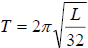 where T is the time in where T is the time in
seconds and L is the length in feet. Find the length of a pendulum that has
a period of 7.2 seconds.
75. The formula for the distance required of a moving object to reach a specific
velocity is
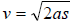 where v is the velocity of the object, a is
the acceleration of the object and s is where v is the velocity of the object, a is
the acceleration of the object and s is
the distance required. What distance is required for an car to reach a velocity
of 50 miles per
hour if the acceleration is 5 miles per square second?
76. The formula for the distance required of a moving object to reach a specific
velocity is
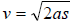 where v is the velocity of the object, a
is the acceleration of the object and s is where v is the velocity of the object, a
is the acceleration of the object and s is
the distance required. What distance is required for an car to reach a velocity
of 72
kilometers per hour if the acceleration is 10 kilometers per square second?
77. The formula for the demand for a certain product is given by
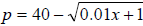 where x where x
is the number of units demanded per day and p is the price per unit. What is the
demand if
the price is $37.55?
78. The formula for the demand for a certain product is given by
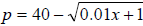 where x where x
is the number of units demanded per day and p is the price per unit. What is the
demand if
the price is $34.70?
79. The formula for the escape velocity of a satellite is
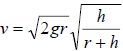 where v is the velocity, where v is the velocity,
g is the force of gravity, r is the planets radius and h is the height of the
satellite above the
planet. What is the height above the Earth would the Space Shuttle be if the
gravitational
pull is 0.0098 km/sec2 and the escape velocity is 2.45 km/sec? (The radius of
the earth is
about 6440 km)
80. The formula for the escape velocity of a satellite is
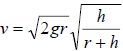 where v is the velocity, where v is the velocity,
g is the force of gravity, r is the planets radius and h is the height of the
satellite above the
planet. What is the height above the Earth would a satellite be if the
gravitational pull is
0.0098 km/sec2 and the escape velocity is 1.25 km/sec? (The radius of the earth
is about
6440 km)
|