Division of Radicals
In this section we want to talk about how to divide radicals, thereby
completing all of our basic operations on radicals.
First we need a property and we need to recall what it means for a radical to
be in simplest form.
| Quotient Property of Radicals |
If
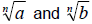 are real numbers then,
are real numbers then,
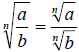 |
Recall the following from section 8.2.
| A radical is in simplest form when: |
1. The radicand has no factors that have a power greater than the
index.
2. No fractions are underneath the radical.
3. No radicals are in the denominator. |
We have already learned how to deal with the first part of this rule. We now
need to deal with the second and third parts. It should be clear that to deal
with the second part (No fractions are underneath the radical) we simply use the
quotient property of radicals stated above. However, to deal with the last part
is a little more complicated.
Example 1:
Simplify.

Solution:
a. We start by using the quotient property to break the radical over the
fraction. Then we simplify numerator and denominator individually as before.
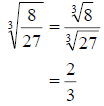
b. We proceed the same as in part a. Use the quotient property and then
simplify.
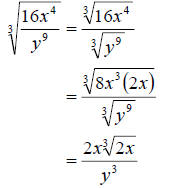
Since there is no radical in the denominator and all the powers are smaller
then the index we have fully simplified the radical.
In the example we should notice that the denominators were set up very nicely
for us in the sense that the radical completely simplified so that there was no
radical left in the denominator.
However, what happens if we have a problem like
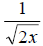 .
Clearly the radical in the denominator .
Clearly the radical in the denominator
is already simplified. But to simplify the entire fraction we need to find a
way to get the radical out of the denominator. To do this we do something called
rationalizing the denominator.
| To rationalize the denominator we multiply the numerator and
denominator by something that will clear the radical from the
denominator. |
We will need to call upon all that we have learned thus far about radicals to
do this rationalizing the denominator.
Example 2:
Simplify. Be sure to rationalize the denominator.

Solution:
a. To rationalize the denominator we need to multiply the numerator and
denominator by whatever it takes to get the radical to drop off. In this case we
can use
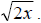 Since we can notice that
Since we can notice that
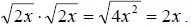 So
we proceed as follows So
we proceed as follows
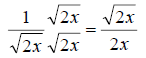
b. Here we need to start by breaking up the radical over the numerator and
denominator. Then we should simplify the numerator and denominator separately.
We get
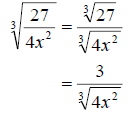
Now we notice that we have a radical in the denominator. Therefore we must
rationalize the denominator. The key is multiply numerator and denominator by a
radical containing enough to make the exponents on the inside match the index.
This works since we know that if the index and the power match then they cancel.
So in this case we will need to use
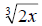
since 4 = 22. We get
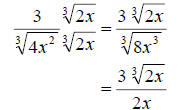
Now the radical is completely simplified.
c. Again, we will split the radical to begin the problem. This time, however,
we will need to simplify both numerator and denominator before we think about
rationalizing the denominator. We proceed as follows.
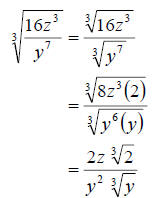
Now we need to rationalize the denominator. Remember, we will need to
multiply by whatever it takes to get the radicand to have a 3rd power (so that it
will match the index).
We see clearly we will need a
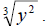 So we get So we get
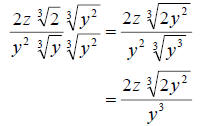
We can do no more reducing. Therefore the radical is
completely simplified.
d. Lastly, we notice that the radical in this example does
not simplify. Therefore we will merely have to rationalize the denominator and
reduce. Since this time we have an index of 4, we will need to make each value
in the radicand have a 4th power. We know that 4 = 22. So
we clearly use 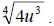 We get We get
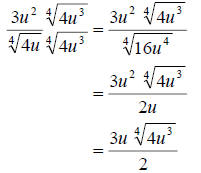
In the last step we canceled a u on top and bottom since
they we both outside the radical. We must always make sure we do any canceling
that is possible to ensure that we end up in simplest form.
So we see that the key to rationalizing a denominator is
multiplying the numerator and denominator by a radical of the same index, whose
radicand will make the total radicand have the same powers as the index. This
will guarantee that the radical on the denominator will simplify leaving no
radicals on the denominator as desired.
What about if we have an expression like
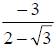 ? We clearly cannot use the same technique
since there are two terms in the denominator and we would have to distribute to
both terms. ? We clearly cannot use the same technique
since there are two terms in the denominator and we would have to distribute to
both terms.
So we recall the following.
| Definition: Conjugates |
The expressions
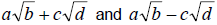 are called conjugates. Conjugates
always have a product that is “radical free”. are called conjugates. Conjugates
always have a product that is “radical free”. |
So, since the product of the conjugates always has no
radicals, we can use it to rationalize any denominator that has two terms.
We can simply multiply numerator and denominator by the
conjugate of the denominator to rationalize the denominator.
Example 3:
Simplify.
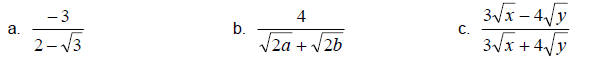
Solution:
a. So as we said above we need to multiply the numerator and denominator by the
conjugate of the denominator. The conjugate of the denominator is
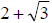 . So we get . So we get
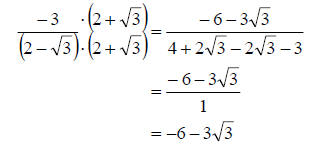
b. Again, we rationalize the denominator by multiplying
the numerator and denominator by the conjugate of the denominator,
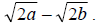 This gives us This gives us
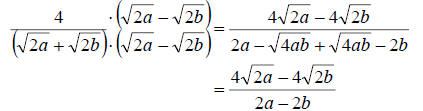
Notice that each term in the numerator and denominator has
a 2 in common. This means we can factor it out of both and then cancel the two
out to completely reduce the expression. We get
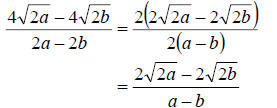
Now that we have no more common factors and all radicals
are simplified, the expression is completely simplified.
c. Lastly, we rationalize as we did above.
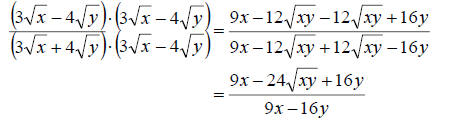
Since the operation on the numerator and denominator is
subtraction, we cannot cancel the 9x or the 16y. Remember, we can only cancel
under the operation of multiplication. So we have fully simplified the
expression.
8.5 Exercises
Simplify. Be sure to rationalize all denominators.

|