Roots, Radicals, and Root Functions
• Definition of radical expressions
• Graphing radical expressions
• Rational exponents and their relationship to radicals
• Simplifying radical expressions; addition, subtraction, multiplication,
division
• Solving radical equations
• Complex numbers
Section 10.1: Radical Expressions and Graphs
• Square Roots
• Cube Roots
• Fourth Roots
• 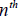 Roots Roots
Square Roots of a
If a is a positive real number, then
1. 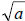 the positive or principle square root of
a the positive or principle square root of
a
2.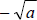 the negative square root of a the negative square root of a
For nonnegative a
1. 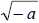 not a real number; it is a complex number not a real number; it is a complex number
2. 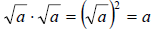
3. 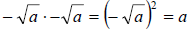
Also, 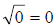
Examples: Find each square root.
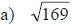
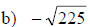
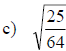
Examples: Find the square of each radical
expression.
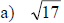
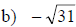
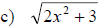
Notes:
• If a is a positive real number that is not a perfect
square, then 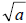 irrational irrational
• If a is a positive real number that is the square of a
number, then 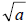 rational rational
• If a is negative real number then,
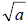 a complex number or a non real number a complex number or a non real number
Examples: Determine whether each square root is
rational, irrational or not a real number.
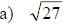
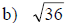
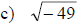
Examples: Find each root.
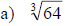
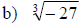
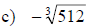
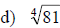
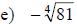
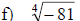
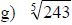
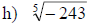
Graphing Functions Defined by Radical Expressions
• Use a table of values to find points which satisfy the
function
• The domain of radical expressions is all values for
which the radical is defined
• In radicals with an even index, the radicand must be
nonnegative
• In radicals with an odd index, the radicand can be
wither positive or negative
Examples: Graph the following radical functions.
Give the domain and range in each case.
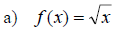
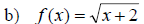
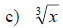
Simplifying nth Roots
• If n is an even positive integer, then
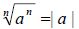
• If n is an odd positive integer, then
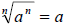
Examples: Simplify each root.
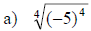
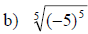
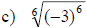
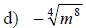
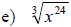
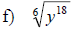
Section 10.2: Rational Exponents
• Relationship between exponents and radicals
• Radicals can be written as rational exponents
Note: If 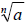 a real
number, then a real
number, then 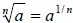
Examples: Evaluate each exponential. Rewrite as a
radical.
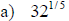
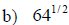
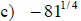
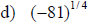
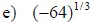
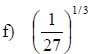
Properties
1. If m and n are integers with
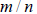 in lowest terms, then in lowest terms, then
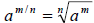
2. If 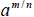 is a real number,
then is a real number,
then 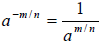
If all indicated roots are real numbers, then
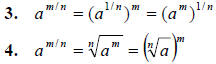
Examples: Simplify each exponential. Rewrite as a
radical
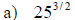
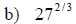
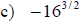
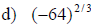
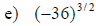
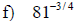
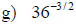
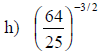
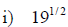
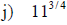
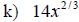
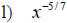
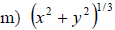
Examples: Write each radical as an exponential.
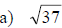
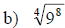
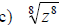
Rules of Exponents
1. Product Rule: 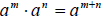
2. Zero Exponent:
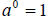
3. Negative Exponent:
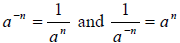
4. Negative Exponent with Fractions: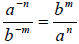
5. Quotient Rule:
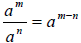
6. Power Rules:
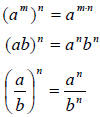
Examples: Fully simplify the given expressions.
Write with only positive exponents. Assume
that all variables represent positive real numbers.
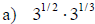
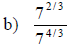
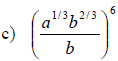
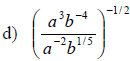
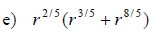
Section 10.3: Simplifying Radical Expressions
• Methods used to simplify radical expressions
Product Rule
• If 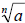 and and
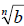 are real numbers and n is a natural number,
then are real numbers and n is a natural number,
then
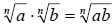
• The product of two radicals is the radical of the
product
Quotient Rule
• If 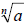 and and
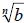 are real numbers, with are real numbers, with
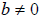 and n is a natural number, then and n is a natural number, then
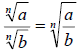
• The radical of the quotient is the quotient of the
radical
NOTE: We can only use the product rule and the
quotient rule when the index on the radicals is the same
|