Exponents and Radicals
2.3. Radicals
Life would be very tiresome if all we did in mathematics is to raise
one number to an integer power. Let’s strive forward and take up the
concept of a root of a number.
Let n ∈ N be a natural number and a ∈ R be a
real number. The nth
root of the number a is defined as follows.
Case 1: n is an odd number. In this case the nth root of a is
defined to be that number b ∈ R such that bn = a. In this case,
write
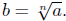 Thus, Thus,
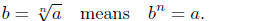 (4) (4)
Case 2: n is an even number. In this case, the nth root of a is
defined to be that number b ≥ 0 such that bn = a. In this case,
write
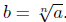 Thus, Thus,
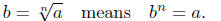 (5) (5)
Note: If a < 0, then there is no number b ≥ 0 that satisfies
(5).
Even roots exist only for nonnegative numbers.
The expression
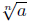 is called a radical and a is referred to as the is called a radical and a is referred to as the
radicand.
In the age of the electronic calculator, computing roots is trivial
pursuit—actually you aren’t computing roots you are approximating
the roots. Therefore, we shall concentrate on the more algebraic or
symbolic properties of radicals. But first, let’s take a look at some
simple examples and accompanying comments.
Illustration 11. There are a few numerical examples.
(a) (Case 1.) The odd root of any number exists: For example,
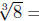
2, since 23 = 8; and
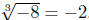 , since (−2)3 = −8. , since (−2)3 = −8.
(b) (Case 2.) The even root of a negative number does not exist (as
a real number). Thus,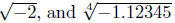 do not exist as real do not exist as real
numbers. (Note: they do exist as complex numbers).
(c) (Case 2.) The even root of a nonnegative number exists: For
example,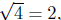 since 22
= 4; and since 22
= 4; and
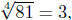 since 34 = 81. since 34 = 81.
Note that the even root is defined to be a nonnegative number. Here’s
an important point. By definition, the
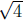 is that number b that satisfies is that number b that satisfies
three conditions:
(1) b ∈ R
(2) b ≥ 0
(3) b2 = 4.
The student no doubt knows that there are two numbers b that satisfy
(1) and (3). The numbers 2 and −2 both have the property that their
square is 4; however, only 2 satisfies all three conditions. It is 2 that
we designate as
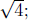 that is, that is,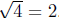 The number −2 is not referred The number −2 is not referred
to as the square root of 2.
Sometimes we want to access both numbers. For example, suppose
we want to find all solutions to the equation b2 = 33. The correct
way of designing all solutions is
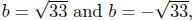 or simply as or simply as
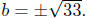
One last comment. Odd roots always exist and have the property that
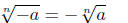 for n odd. (6) for n odd. (6)
This is a quite useful simplifying tool. The equalities
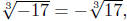
and
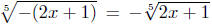 are two examples of the use of this are two examples of the use of this
property.
• Properties of Radicals
When manipulating algebraic quantities, we often want to manipulate
expressions involving radicals.
Let’s begin with a quiz.
Quiz. Think about each of these questions before responding. When
you click on the correct answer, you will jump to a discussion
1. Which of the following is a correct simplification of
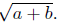

2. Let a ∈ R and n ∈ N a natural number. Is it (always) true that
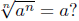
(a) True (b) False
End Quiz.
Properties of Radicals:
Let a, b ∈ R be real numbers, and n, m ∈ N be natural
numbers, then1.
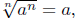 if n is odd, and
if n is odd, and
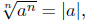 if n is even. if n is even.
2.
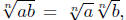 if n is odd, or if n is even, provided if n is odd, or if n is even, provided
a ≥ 0 and b ≥ 0.
3.
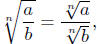 if n is odd and b
≠ 0, or if n even, provided if n is odd and b
≠ 0, or if n even, provided
a ≥ 0 and b > 0.
4.
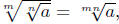 if m and n are both odd; otherwise, a if m and n are both odd; otherwise, a
must be nonnegative (a ≥ 0). |
Let’s take a brief look at each of these in turn.
■ The First Property of Radicals. The first stated property is
usually no problem for students who already have experience working
with radicals. When we are taking an odd root then
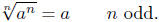
For example,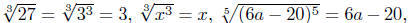 and and
so on.
However, if we are taking an even root, then we must be a little more
circumspect. The basic formula is

Recall that an even root is always nonnegative; hence, the necessity
for the absolute values.
We have no problems if a is positive. The case where a < 0 is the
problem child. For example
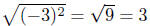
Notice that from this computation,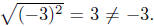 Of course, 3 Of course, 3
is related to −3 by | − 3| = 3. Thus we have shown in this example
that
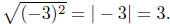
Illustration 12. Consider the following phalanx of examples.
(a)
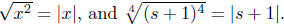
(b)
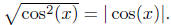
(c) If we have information related to the sign of the radicand, we
can remove the absolute values.
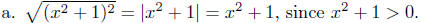
b. Suppose s > 3, then
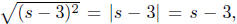 since since
s − 3 > 0.
c. Suppose t < 1, then
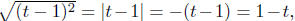
since t − 1 < 0.
Exercise 2.8. Simplify each of the following using the
Properties of
Radicals.
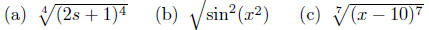
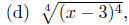 given x < 3. given x < 3.
Not all expressions are of the form nth roots of nth powers. An important
variation is
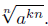
That is, a is raised to an integer, k, multiple of n. The evaluation of
this root depends on whether n is odd or even and can be successfully
carried out by the application of the Laws of Exponents.
Illustration 13. Consider the following.
(a)
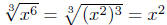 since since
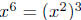 by the Law of Exponents, by the Law of Exponents,
Law 3.
(b)
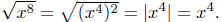 We inserted absolute values because We inserted absolute values because
we are extracting an even root. But since x4 ≥ 0, we can, in turn,
evaluate the absolute value to x4.
(c)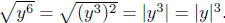 Here, y3 may be positive or nega-tive Here, y3 may be positive or nega-tive
so we cannot remove the absolute values without information
about the sign of y.
■ The Second Property of Radicals. This property is very
frequently used; care must be made not to abuse it. Property 2 states
that “a root of a product is the product of the roots, if n is odd, or if
n is even, provided all factors are nonnegative.”
The bad case is when a < 0 and b < 0 and we are taking an even root
of ab; in this case,
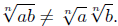
To see this, put n = 2, a = −1 and b = −1, to get
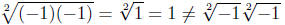
We run into problems when we take an even root of a negative number.
(A no, no.) This is rather obvious, but becomes less obvious when
dealing with symbolic quantities. Whenever you are tempted, for example,
to simplify an expression like
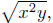 you must be very careful you must be very careful
not to write
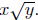
Quiz. What is the simplification of
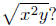
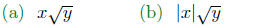 (c) I cannot be simplified
(c) I cannot be simplified
This second property is used, in combination with the first property
of radicals to extract perfect roots.
Illustration 14. Extract perfect roots.
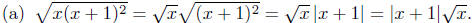
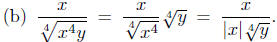 (No additional simplification is (No additional simplification is
possible unless more information is known about the sign of x.
1. If it is known that x ≥ 0, then |x| = x and so
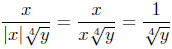
2. If it is known that x < 0, then |x| = −x and so
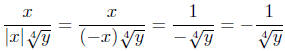
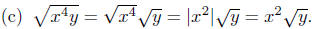
(d) In this example, more detail is presented.
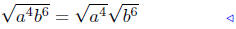 |
Prop. Rads. #2 |
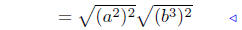 |
Law Exp. #3 |
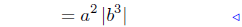 |
Prop. Rads. #1 |
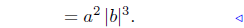 |
A Prop. Abs. Value #2 |
Illustration Notes: Illustration (d) is a good illustration how the various
properties of exponents, of radicals, and of absolute values are
utilized. When you become an expert, this simplification would be
just a single step, not four steps as I have above.
Property #2 can also be used to partial extraction. Let me illustrate
what I mean.
Illustration 15. Study the following examples.
(a)
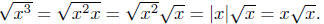 . In the last equality we . In the last equality we
were able to remove the absolute value symbols. Why?
(b)
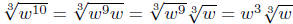
■ The Third Property of Radicals. This property is the same
as #2, but for quotients. Just two examples are sufficient.
Example 2.1. Simplify the following: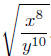
Example 2.2. Simplify
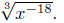
Exercise 2.9. Simplify each of the following utilizing the Properties
of Radicals, the Laws of Exponents, and properties of Absolute Value.
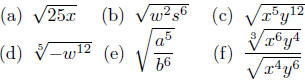
■ The Fourth Property of Radicals. This law describes what
a root of a root is; it’s . . . another root! Let’s work it out. We want
to understand the simplification of
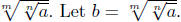 The characteristic The characteristic
property of b is that
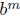 = the radicand =
= the radicand =
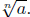 Now if Now if
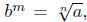 then by the definition,
then by the definition,
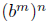 = the radicand = a. Thus, = the radicand = a. Thus,
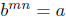 But this is the definition of b being the mnth root of a; i.e., But this is the definition of b being the mnth root of a; i.e.,
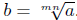 We have shown that We have shown that
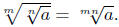
Illustration 16.
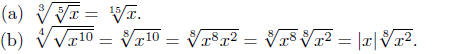 (7) (7)
• Question Argue that
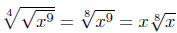
is true. Compare this equation with (7) and explain why the absolute
value is not needed.
|