Exponents and Radicals

Table of Contents
2. Exponents and Radicals
2.1. Integer Exponents
2.2. The Law of Exponents
• How to Multiply or Divide Two Powers • How to Calculu-ate
a Power of a Product or Quotient • How to Compute
a Power of a Power
2.3. Radicals
• Properties of Radicals
2.4. Fractional Exponents
2. Exponents & Radicals
This lesson is devoted to a review of exponents, radicals,
and the
infamous “Laws of Exponents.” The student must have the skills to
manipulate exponents without error.
2.1. Integer Exponents
Let a be a number, and n ∈ N be a natural number. The symbol an
is defined as
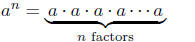 (1) (1)
That is, an is the product of a with itself n times.
Sometimes, negative exponents enter in to the mix. These
are defined
by
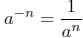 where n ∈ N and a ≠ 0. (2)
where n ∈ N and a ≠ 0. (2)
Needless to say, we define a0 = 1, for all a ≠ 0.
Thus, the symbol ak is defined for all integers k ∈ Z:
for positive
integers as in equation (1), 23 = (2)(2)(2) = 8; for negative integers
as in equation (2), 2-3 = 1/23 = 1/8; and for zero, 20 = 1.
Terminology. The symbol a^k is called a power of a.
We say that a^k
has a base of a and that k is the exponent of the power of a.
Numerical calculations offer no challenge to the student (that’s you).
The more interesting case is when there are symbolic quantities involved;
however, there is one situation involving numerics (and sym-bolics)
in which some students—I’m not saying you necessarily—have
a weakness. Consider the following . . .
Quiz. Suppose you wanted to square the number −3, what would be
the correct notational way of writing that?
(a) −32
(b) (−3)2
(c) (a) and (b) are equivalent
To effectively manipulate expressions involving symbolics, we must
be the masters of the Laws of Exponents—to be taken up shortly;
just now, however, I want to illustrate how the definitions of a^k are
applied.
Illustration 1. Here are several important illustrations of the techniques
revolving about the definitions given in equations (1) and (2).
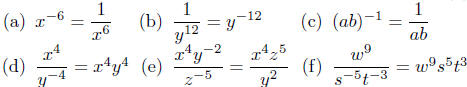
Illustration Notes: Look at (a) first from left-to-right. Basically, this
says that if we have a negative exponent in the numerator, we can
shove the expression into the denominator by changing the sign of
the exponent. Reading (a) from right-to-left, we see that if we have
an expression in the denominator, we can lift it to the numerator by
changing the sign of the exponent. Similar comments can be made in
equation (b).
■
Illustration (c) suggests that if an expression is grouped, then
when we move it to the denominator, we move the whole group.
■
Examples (d), (e) and (f) demonstrate how equations (1) and
(2) are used in practice. Note that these expressions only involve
multiplication
and/or division—most important!
■ Key Point. When moving expressions from the numerator to the
denominator (or from denominator to numerator), simply change the
sign of the exponent.
■ Important. The last point is only valid for expressions involving
multiplication and/or division. For example, the following shall be
referred to as an algebraic blunder!
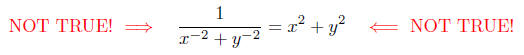
Exercise 2.1. Remove all negative exponents for each of the expressions
below.
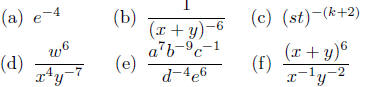
|