Simplifying Radicals

In order to simplify a radical we must understand the concept of “perfect powers”. A radicand is said to be a perfect power when the exponent of the radicand is a multiple of the index of the radicand. To determine if a radicand is a perfect power for a given index, simply divide the exponent of the radicand by the index to check if the result is an integer.

For example, in the radical 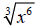the radicand is a perfect power because the exponent “6” is a multiple of the index “3”.

6 ÷ 3 = 2; since 3 divides evenly into 6 the radicand is a perfect power.

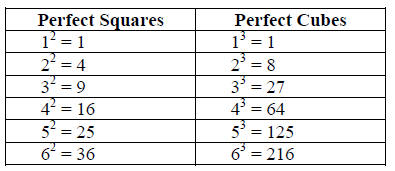
Knowing the perfect squares and cubes will help in simplifying the radicals when used in conjunction with the product rule for radicals. The product rule of radicals states that the product of two radicals is equal to the radical of their product for nonnegative real numbers a and b, and integer n > 1

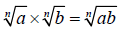
Note that the indexes on the radicals are not multiplied together. Only the radicands are multiplied together.

Example 1: Simplify

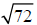
Solution:
Step 1: Factor 72 as the product of a perfect square and another integer

The largest perfect square that is a factor of 72 is 36

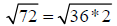
Step 2: Use the product rule for radicals to separate the radical into a product of
radicals

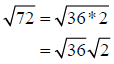
Step 3: Simplify the radical

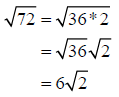
Example 2: Simplify

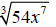
Solution
Step 1: Factor 54x^7 as the product of a perfect cube and another term

The largest perfect cube that is a factor of 54 is 27
The largest perfect cube that is a factor of x^7 is x^6

So our perfect cube will be 27x^6
Which would leave 2x as our other product in the radicand

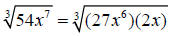
Step 2: Use the product rule for radicals to separate the radical into a product of
radicals

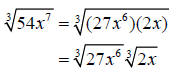
Step 3: Simplify the radical

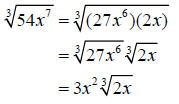
If you are having difficulty reducing the radicals then there is another method you can use to determine what will come out of the radicand and what will remain inside. The method involves dividing the exponents of each term by the index. The quotient will be the exponent of the term that will go outside of the radicand and the remainder will be the exponent of the term left inside the radicand.

Let’s use the cube root of 16x¹⁷y⁸ as an example.
First, we will rewrite 16 in its prime factorization form of 2⁴

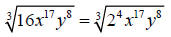
Now, divide each exponent by the index

The quotients will be the exponents on the terms outside the radicand and the
remainders will be the exponents inside the radicand.

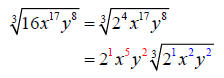
Last, simplify the exponents.

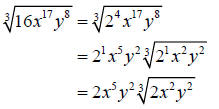
Example 3: Simplify 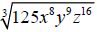using the quotient/remainder method.

Solution:
Step 1: Rewrite 125 in its prime factorization form

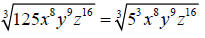
Step 2: Divide each exponent in the radicand by the index

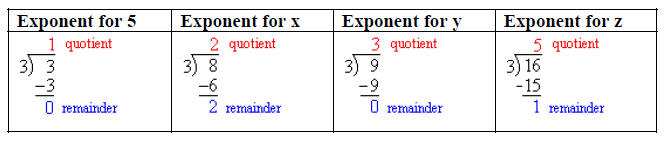
Step 3: Place the quotients as exponents outside of the radicand and the remainders
inside.

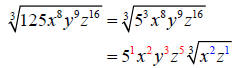
Step 4: Simplify

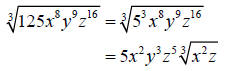
Another rule that will come in assistance when simplifying radicals is the quotient rule for radicals. Like the product rule, the quotient rule provides us with a method of rewrite the quotient of two radicals as the radical of a quotient or vice versa provided that a and b are nonnegative numbers, b is not equal to zero, and n is an integer > 1.

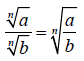
Example 4: Simplify

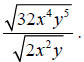
Solution
Step 1: Use the quotient rule of radicals to rewrite the problem as the radical of a
quotient.

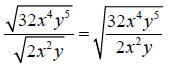
Step 2: Reduce the fraction inside the radicand

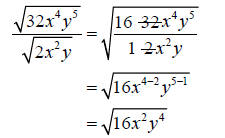
Step 3: Rewrite 16 in prime factored form

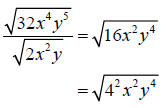
Step 4: Simplify the radical
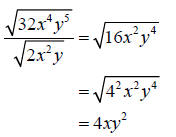