Working with Radicals and Roots
A radical expression is an expression that involves the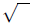 sign.
The number sign.
The number
under the radical sign is called the radicand. The index is the small number
written
in the "V" of the radical sign and it tells us the "root" of the expression. If
the index
is not written, then it is assumed to be two, and the radical is a square root.
In
general,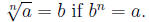 For example: For example:
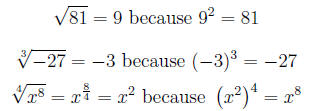
There are two special rules for radical expressions with
even indexes, i.e. "even
roots."
•The even root of a quanity is always assumed to be
positive, i.e. 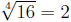 even even
though -2 could also be an answer.
•There is no real even root of a negative number, i.e.
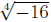 is not a real number is not a real number
because there is no real number that you can multiply by itself four times and
get -16.
•Simplifying an nth Root:
1. Write the coefficent as a product of two numbers where
one is the largest
perfect nth power that divides the coefficent. Note that this may take
some trial and error. Start with the smallest perfect power, 2n, and you
can stop once the the result of the division is larger than the number you
are dividing by.
2. For each expression that is raised to an exponent,
split the expression into
a product of two powers where one power is a perfect power, i.e. a multiple
of n, and one power is a number less than n.
3. Use the fact that 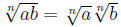 to rewrite the radical as a product of two
to rewrite the radical as a product of two
radicals. One radical should only contain the perfect powers.
4. Simplify the radical of perfect powers.
Example 1 Simplify
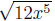
1. The coefficent is 12, and the largest perfect square that
divides 12 is 4, so
write 12 as 4 * 3.
2. x is raised to the fifth power. The largest multiple of
two that is less than
five is four, so we will write 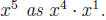
3. Our radical now becomes:
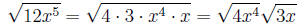
4. Simplifying the first root, we have
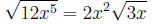
Example 2 Simplify
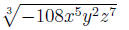
1. The coefficent is -108, and the largest perfect cube that
divides -108 is
-27, so write -108 as -27 * 4.
2. x is raised to the fifth power. The largest multiple of
three that is less than
five is three, so we will write 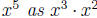 . y is raised
to the second power. . y is raised
to the second power.
Two is less than three, so there is no perfect cube that divides y^2. z is
raised to the seventh power. The largest multiple of three that is less than
seven is six, so we will write 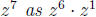 . .
3. Our radical now becomes:
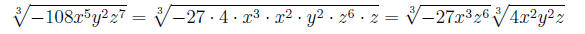
4. Simplifying the first root, we have
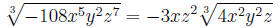
•Arithmetic with Radicals: You may only add or subtract
two radicals if
they are "like terms", i.e. they have the same index and the same radicand.
When you multiply two radicals of the same index together, you can combine
them into one radical by multiplying the radicands, i.e. for a and b
non-negative
numbers, 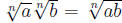 . Similarly, when you divide two
radicals of the same . Similarly, when you divide two
radicals of the same
index together, you can combine them into one radical by dividing the radicands,
i.e. for a and b non-negative numbers,
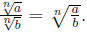
Example 3 Simplify the expression:
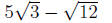
First, simplify the radicals as much as possible.
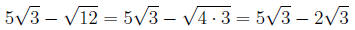
Now, we have like terms, so we can combine:
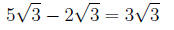
Example 4 Simplify the expression:
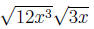
Combining the radicals, we have:
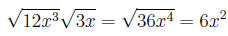
Example 5 Simplify the expression:
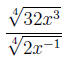
Combining the radicals, we have:
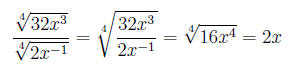
Example 6 Simplify the expression:
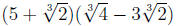
"FOIL"ing out and simplifying, we have:
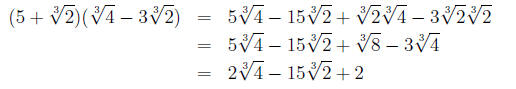
•Rationalizing a Denominator: A fraction is not
considered simplified unless
there are no square roots in the bottom of the fraction. The process of removing
the square roots from the denominator is called rationalizing the denomina-
tor. If the denominator involves a single term, multiply the top and bottom of
the fraction by the square root in the denominator. If the denominator involves
two terms, multiply the top and bottom of the fraction by the conjugate of
the denominator.
Example 7 Rationalize the denominator in the
expression:
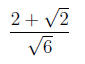
We'll start by multiplying the top and bottom of the
fraction by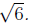 This will not This will not
change the value of the expression since we are simply multiply by an expression
that is equivalent to one. Then we will simplify our answer.
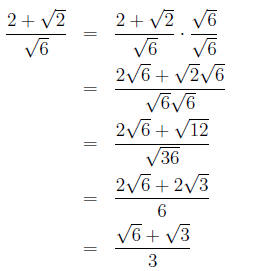
Example 8 Rationalize the denominator in the
expression:
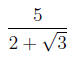
We'll start by multiplying the top and bottom of the
fraction by the conjugate
of the denominator. Since the denominator is 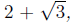 the conjuagte of the
the conjuagte of the
denominator is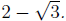 Then we will simplify our
answer. Be sure to "FOIL" Then we will simplify our
answer. Be sure to "FOIL"
out the denominator.
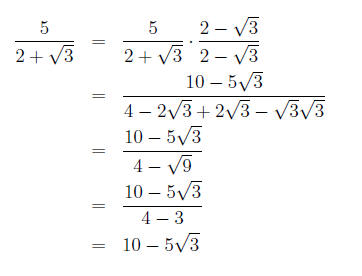
•Problems to Try!! Simplify the following expressions.
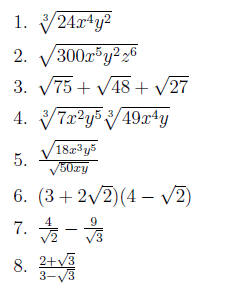
•Answers:
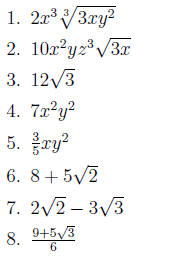
|