Radicals and Rational Exponents
Chapter 7, Section 3: Radicals and Rational Exponents
Suppose that m and n are integers and that there are no
zero divisors. Complete
the following:
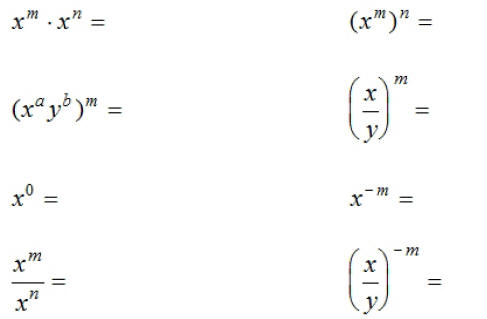
Calculator Activity: Use your calculator to evaluate each
of the following.
Compare
the answers.
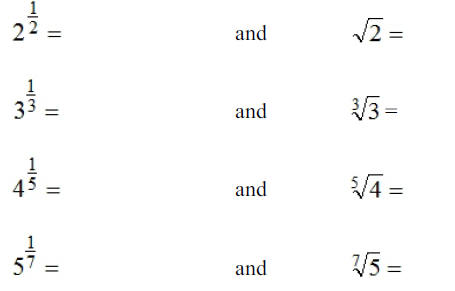
If n is a natural number greater than 1 and
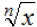 is a real number, then is a real number, then
Question: When is 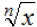 not
a real number? not
a real number?
Rewrite each of the following in radical form and
simplify:
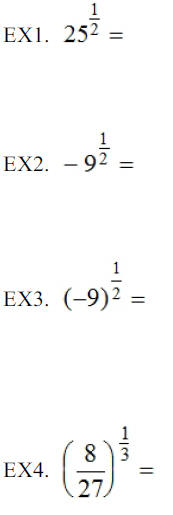
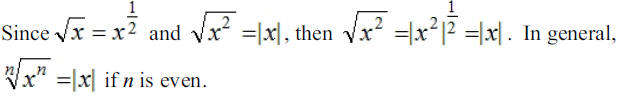
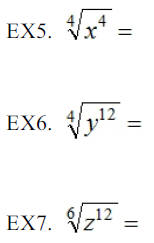
If m and n are positive integers and the GCF (m,n)=1 and
x>0,
then
EX8. Evaluate 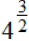 in 2
different ways. in 2
different ways.
1)
2)
EX9. Evaluate 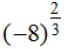 in 2
different ways in 2
different ways
1)
2)
Changing from radical to exponential form and vice versa:
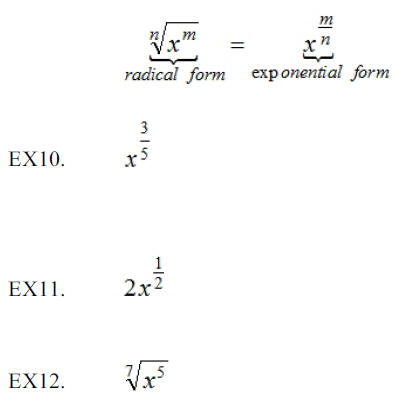
Simplifying Expressions Involving Rational Exponents:
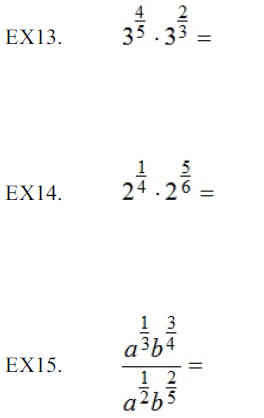
Simplifying Radical Expressions by Reducing the Index
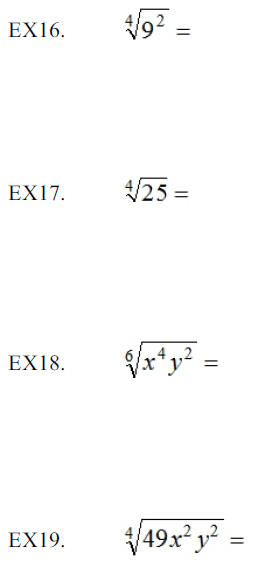
Chapter 7, Section 6: Radical Equations
EX1. Solve: 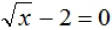 by
inspection; i.e., just determine logically what by
inspection; i.e., just determine logically what
number or numbers will make this equation a true statement.
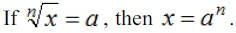
Solve each of the following equations and check your
answers.
Question: Why is it important to check your answers when
solving radical
equations?
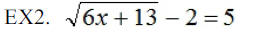
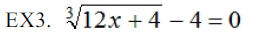
Note: When solving an equation containing 2 or more
radical terms, you need to
remember that 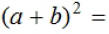
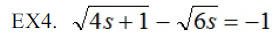
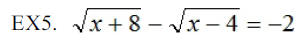
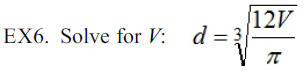
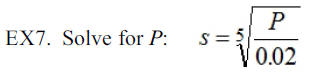
EX8. Find the value of r when n = 5, V = $1338.25, and P =
$1000.
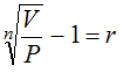
Chapter 7, Section 7: Complex Numbers
EX1. Solve: 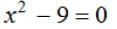
EX2. Solve: 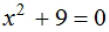
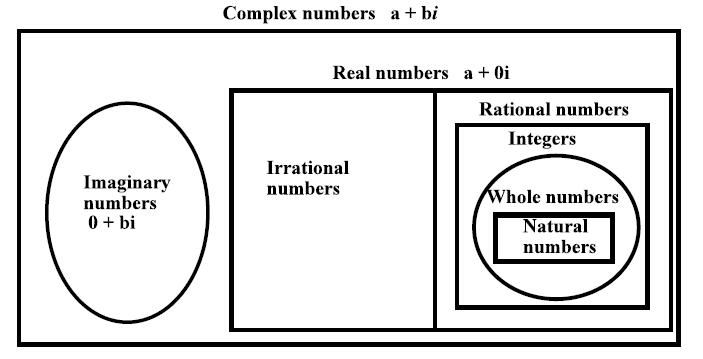
A complex number is any number of the form a+bi
where a and b are real
numbers and 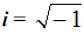 . Note: . Note:
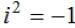 . .
Adding and Subtracting Complex Numbers
EX3. ( 2 + 3i ) + ( 4 - i ) =
EX4. ( 5 - 2i ) + ( -3 - 4i ) =
EX5. ( 2 + 3i ) - ( 4 - i ) =
EX6. ( 5 - 2i ) - ( -3 - 4i ) =
Multiplying Complex Numbers
EX7. ( 2 + 3i )( 4 - i ) =
EX8. ( 5 - 2i )( -3 - 4i ) =
The conjugate of the complex number
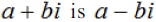 . This is denoted by . This is denoted by
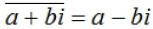 . .
Dividing Complex Numbers: [Note–To divide complex numbers,
multiply both
the numerator and the denominator by the conjugate of the denominator.]
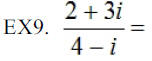
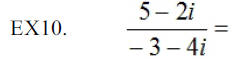
Simplifying the expression where
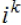 is an integer: is an integer:
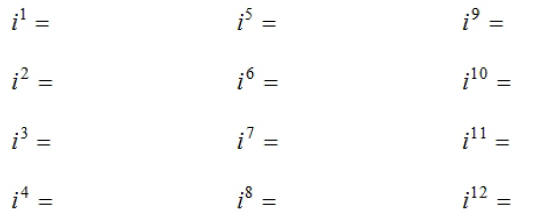
Do you observe any pattern? If so, what is it?
Divisibility Rule for 4: A number N is divisible by 4 if
and only if the
number
represented by the last 2 digits of N is divisible by 4.
EX11. Is 3724 divisible by 4? Why?
EX12. Is 5817 divisible by 4? Why?
EX13. Simplify: 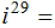
EX14. Simplify: 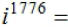
EX15. Suppose that 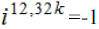 , where k is the units
digit in the exponent. What digit(s) could k be? , where k is the units
digit in the exponent. What digit(s) could k be?
Chapter 8, Section 1: Solving Quadratic Equations by
Completing the Square
Solve: 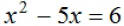 by
factoring. by
factoring.
Solve: 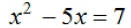 by factoring by factoring
How is this problem different from the first problem?
The Square Root Property: If
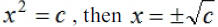
Note: If 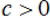 , then there
are ___________________________________. , then there
are ___________________________________.
If 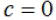 , then there is
____________________________________. , then there is
____________________________________.
If 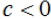 , then there are
____________________________________. , then there are
____________________________________.
EX1. Solve: 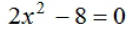
EX2. Solve: 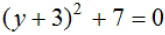
A demonstration of the geometry associated with completing
the square.
What number must be added to each of the following to
complete the square?
Write each perfect square trinomial as a binomial squared.
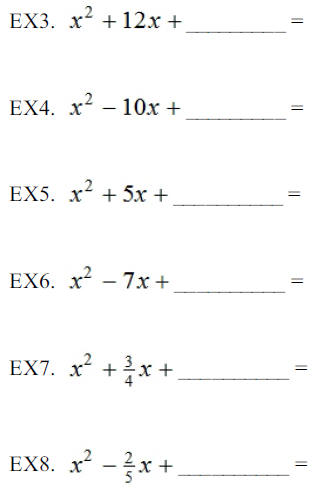
For each of the following, determine a value for k that
would make the trinomial a
perfect square trinomial.
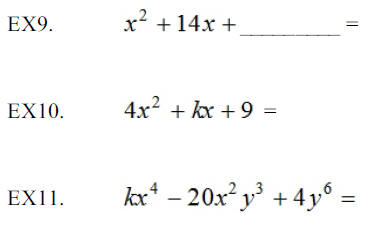
Solve each of the following by the process of completing
the square:
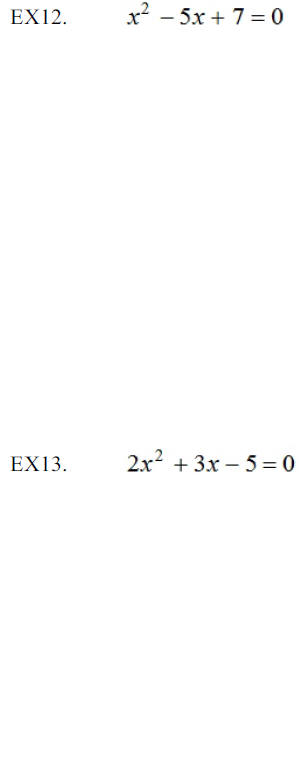
Chapter 8, Section 2: Solving Quadratic Equations by the
Quadratic Formula
EX1. Solve: 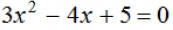 by
completing the square by
completing the square
EX2. Solve: 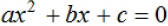 (The General
Quadratic Equation in One (The General
Quadratic Equation in One
Variable) by completing the square.
The quadratic formula is:
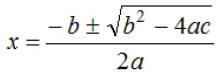
The radicand, 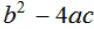 in the
quadratic formula is called the discriminant. in the
quadratic formula is called the discriminant.
If 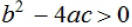 , there are
________________________________________. , there are
________________________________________.
If 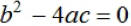 , there is
_________________________________________ . , there is
_________________________________________ .
If 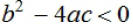 , there are
_________________________________________. , there are
_________________________________________.
Use the quadratic formula to solve each of the following:
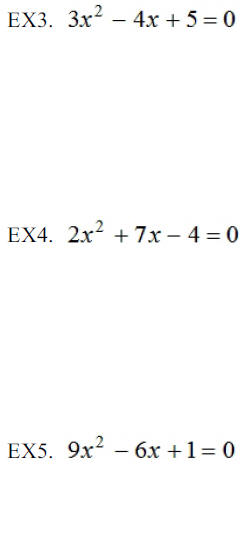
EX6. The product of two consecutive odd negative integers
is 143. Find the
integers.
EX7. A rectangle is 2 inches longer than it is wide.
Numerically, its area exceeds
its perimeter by 11. Find the perimeter of the rectangle.
|