Exponents and Radicals
2.4. Fractional Exponents
Let me finish off Lesson 2 by a (hopefully) brief discussion of fractional
exponents. We begin by making a series of definitions.
Definition. Let a be a number.
1. For n a natural number, define
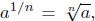 provided the root provided the root
exists as discussed in the definition of radicals.
2. For n a natural number, define
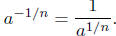
3. If p and q are integers, define
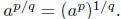 (Of course, we are (Of course, we are
assuming q ≠ 0.)
Illustration 17. Consider the following conversions from radical notation
to exponential notation and from exponential notation to radical
notation.
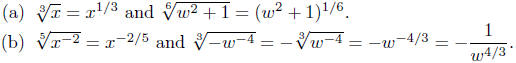
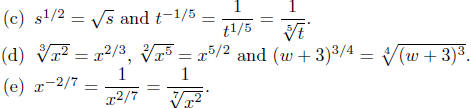
Exercise 2.10. Convert each of the following to exponential notation
using the above definitions.
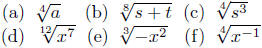
Now let’s convert from exponential to radical notation. Carefully work
out the problems before you look at the solutions. Justify each step
that you make in your solution.
Exercise 2.11. Convert to each to exponential notation.
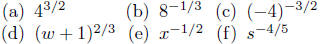
Here’s an important point: The fractional exponent notation is entirely
consistent with reduction of fractions to lowest terms. What do
I mean by that?
Illustration 18. Reduction of Fractional Exponents.
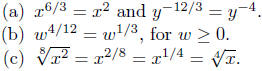
Quiz. Think about each of the following questions before responding.
1. The expression
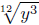 is equivalent to is equivalent to

2. The expression
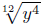 is equivalent to is equivalent to

End Quiz.
The fractional exponent notation is entirely consistent with the Laws
of Exponents. Let’s restate this law for the record.
The Law of Exponents—Senior Grade:
Let a and b be numbers, and r and s be rational numbers,
and assume further that ar and as are defined. Then
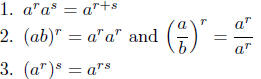
|
All the above equalities are conditional on the existence of each of the
exponentials. For example, (ab)r = arbr is true provided that each of
the exponential (ab)r, ar, and br exist. (Take a look at the second law
above for the case a = −1, b = −1, and r = 1/2—catastrophe!)
Exercise 2.12. Give examples of situations in which Law #1 and
Law #3 are not valid.
In other words, all the techniques outlined and illustrated above applies
to fractional exponents.
Illustration 19. Here are some examples that illustrate the Law of
Exponents—Senior Grade.
1. Law 1: Different exponent, same base; just add exponents.
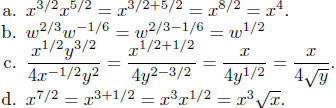
2. Law 2: Same exponent, different base.
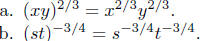 Here, we are taken even roots of s Here, we are taken even roots of s
and t; therefore, we must assume s > 0 and t > 0.
3. Law 3: Nested exponentials, just multiply exponents.
a.
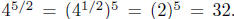 Whereas
Whereas
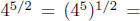
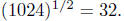 Naturally, the first computation was quite Naturally, the first computation was quite
a bit less complicated; the idea is to choose the order of
calculation that is easiest.
b.
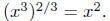
c.
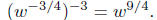
d. Nested radicals are the same as nested exponents, let Exponent
Law #3 handle it.
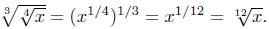
Exercise 2.13. Let n be an even positive integer. Simplify
(an)1/n.
Here are some routine practice exercises for you solve.
Exercise 2.14. Simplify each of the following using the Law of Exponents.
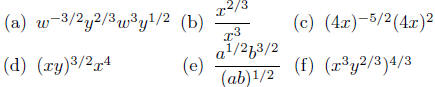
This is the end of Lesson 2! If you have managed to work through
it, you have my congratulations!
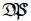
If you are not too exhausted, continue on to Lesson 3. See you there!
Solutions to Exercises
2.1. Passing is 100%!
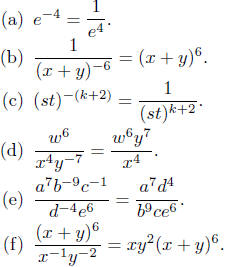 Exercise 2.1. Exercise 2.1.
2.2. And the answers with any further comments are
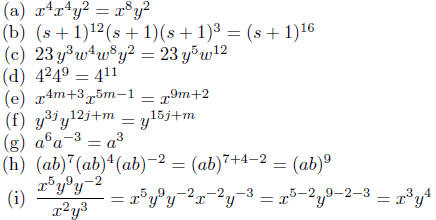
Add the exponents of all exponentials having the same base; bring
factors in the denominator by changing the sign on the exponent,
then add exponents as appropriate. Exercise 2.2.
2.3. Solutions:
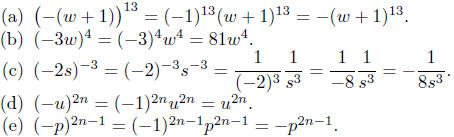
In the last problem, for any given integer n, 2n−1 is an odd integer;
hence,
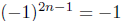 Exercise 2.3. Exercise 2.3.
2.4. Solutions:
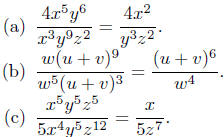
Exercise Notes: In the case of solution (c), we automatically simplified
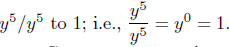
■
Concentrate on using good techniques. Don’t be sloppy. Don’t
revert to your old bad habits. Be precise in all things you do.
Exercise 2.4.
2.5. Answer: Apply Law #2.
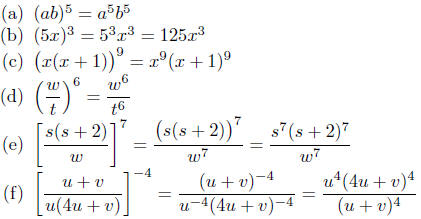
In the last problem, the negative exponents were eliminated by move
them to the numerator or denominator, as appropriate, and changing
the signs of their exponents—standard techniques.
Did you use good notation? Were you neat? Were you organized?
Exercise 2.5.
2.6. Solutions: Apply combinations of Laws #1 and #2.
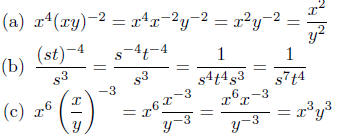
Each of us develop our own pattern of thoughts; whatever patter n
of thinking we develop, ultimately, it must be based on the simple
application of these laws of exponents.
In these solutions, I’ve included a few more steps than is really used
in practice. Exercise 2.6.
2.7. Solutions:
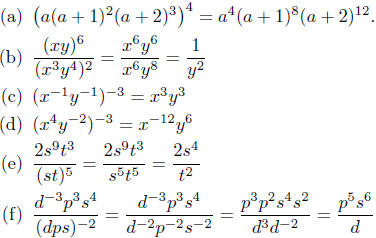
The last example requires a careful application of the Law of Exponents.
Hope you were are careful as I was.
Did you work the problems out first? Were you neat? NOW is the
time to develop good habits . . . not during a test. Exercise 2.7.
2.8. Solutions:
(a)
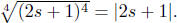
(b)
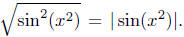 Here the radicand is (sin(x2))2, hence, Here the radicand is (sin(x2))2, hence,
its square root is | sin(x2)|.
(c)
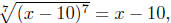 since this is an odd root. since this is an odd root.
(d) Given x < 3,
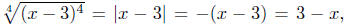 since since
x − 3 < 0. (See definition of absolute value.)
Exercise 2.8.
2.9. Solutions:
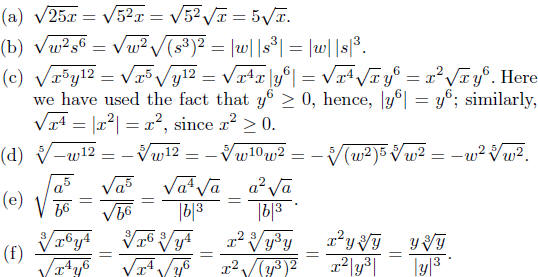
In problem (f), no further simplification is possible without knowledge
of the sign of y. Exercise 2.9.
2.10. Solutions:
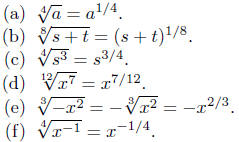
Conversion to exponential must be automatic. Exercise 2.10.
2.11. Solutions:
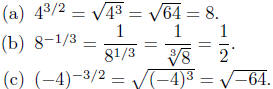 Oops! An even root of a negative Oops! An even root of a negative
number! Therefore,
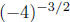 does not evaluate to a real number; does not evaluate to a real number;
It evaluates to a complex number. Did you panic?
Exercise 2.11.
2.12. Law #1. Consider the case a = −1, r = 1/2 and s = −1/2.
In this case,
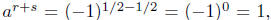 yet yet
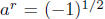 and and
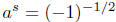 are not defined as a real number. are not defined as a real number.
Law #3. Take a = −1, r = 1/2 and s = 2, then
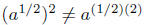
The right-hand side is a1= a = −1, whereas the left-hand side has in
it
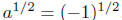 , which is not a real number. , which is not a real number.
In each of the two examples, one of the expressions is not a real number
. . . what’s where we ran into trouble. The Laws are valid whenever
all exponentials are defined. Exercise 2.12.
2.13. This is another exception to Law #3.
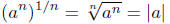
by the (1) of the property of radicals. Thus, if a < 0, then
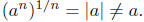
Doesn’t this contradict the third law of exponents? The premise of
the laws of the exponents is that 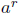 and and
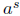 are both defined. In this are both defined. In this
situation, for a < 0, 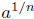 is not defined since we are taking an even is not defined since we are taking an even
root of a negative number; therefore, the Laws of the Exponents does
not guarantee the validity of Law #3. Exercise 2.13.
2.14. Solutions:
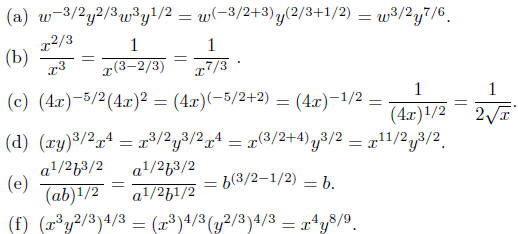 Exercise 2.14. Exercise 2.14.
|