Solving Radical Equations
8.1 Definitions and Roots
▪ Need To Know
▪ How to find the root of a number
▪ Categorizing roots
▪ How to find the root of an expression
▪ How to solve application problems
involving roots
Idea of Square Roots
In mathematics, once we learn an operation,
we also learn the reverse of that operation.
For real numbers x and y,
If y = x2 then x = ___
Don’t Forget
Radicand
Radical Sign
Radical
Definitions and Roots
Definition – If x is any positive real number, then
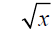 is the square root of x and
is the square root of x and
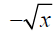 is the square root of x.
is the square root of x.
Examples:
Name the two square roots of 81.
Find the root of
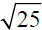
Simplify
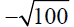
Evaluate
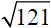
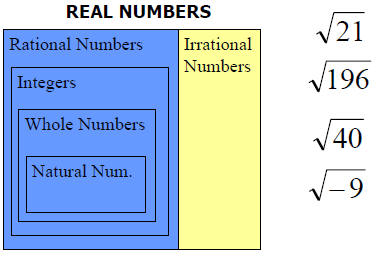
Recall Number Sets

▪ Rational Numbers
are the numbers of
the form a/b where
b is not zero.
▪ Rational Numbers is
the set of all fractions
Recall Number Sets

▪ Irrational Numbers
are the numbers
that can not be
written as fractions
▪ Real Numbers are
the collection of all
Rational and
Irrational Numbers.
Categorize Roots
Square Roots & Absolute Value
Consider
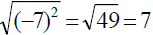 and and
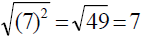
Both come out positive.
Recall: |-7| = 7 and |7| = 7.
For all real numbers A, ___________________
Examples:
Application
The speed of sound in feet per second, V, traveling
through air with a temperature of t is given by the
formula below. Find the speed of sound when the
temperature is 5° C.
8.1 Conclusion
▪ The square root is the number that
“undoes” the square.
▪ Square roots can be positive or negative.
▪ The square root of zero is zero.
▪ The square root of a negative number is
not a Real Number
▪ A square root results in a
Rational, Irrational or Non-Real Number
8.2 Multiply and Simplify Radicals
▪ Need To Know
▪ Multiplying of radicals
▪ Simplifying radical expressions
1. With numbers
2. With variables
Multiplication Property of Radicals
▪ If A and B are real numbers (> 0), then
______________________________
Simplify Radical Expressions
| ▪ Simplify:

|
Perfect
Square

|
Simplify Radical Expressions
| ▪ Simplify:
 |
Perfect
Square
 |
Simplify Radical Expressions
▪ Simplify:
Square roots
undo squares
Practice Simplifying Radicals
▪ Simplify:
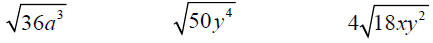
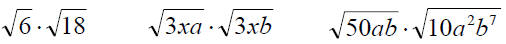 end
end
8.3 Properties of Radicals
▪ Need To Know
▪ Quotient Rule for Square Roots
▪ Simplifying radical expressions
1. With Fractions
2. By Rationalizing the Denominator
Quotient Rule for Square Roots
▪ If A and B are real numbers (B ≠ 0),
then
__________________________________
Simplify Radical Expressions
▪ Simplify:


The Idea of a Simplified Radical
Which fraction is the simplest?
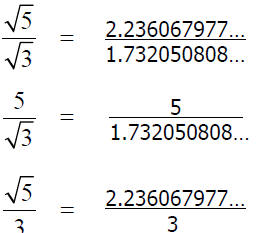
Rationalizing Denominators
▪ Goal: Change the fraction to make the
denominator come out “nice”.
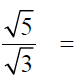
Guidelines for Simplification
1. Remove ____________________________
2. Remove ____________________________
3. Remove ____________________________
▪ Examples:

Guidelines for Simplification
1. Remove fractions from radicals
2. Remove perfects for radicals
3. Remove radicals from denominators
▪ Examples:
 end end
|