Radical Expressions
9.1 Simplify Radical Expressions
Radical Notation for the n-th Root of a
If n is an integer greater than one, then the nth root of a is
the number whose nth power is a. There are two notations
for the nth root of a:
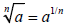
where
n is called the index of the radical
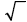 is called the radical symbol is called the radical symbol
a is called the radicand
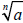 is the radical form of the n-th root
of a is the radical form of the n-th root
of a
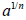 is the exponential form of the n-th
root of a is the exponential form of the n-th
root of a
An expression containing a radical symbol is called a
radical expression. Some examples of radical expressions
are
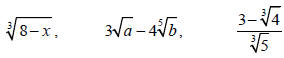
Consider the Sign of the Radicand a: Positive,
Negative, or Zero
1. If a is positive, then the nth root of a is also a positive
number - specifically the positive number whose nth
power is a.
e.g.
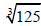 is asking is asking 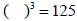
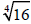 is asking is asking 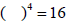
2. If a is negative, then n must be odd for the nth
root of a
to be a real number.
e.g.
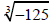 is asking is asking
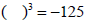
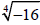 is asking is asking 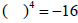
Furthermore, if a is negative and n is odd, then the nth
root of a is also a negative number - specifically the
negative number whose nth power is a.
3. If a is zero, then 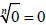 . .
Example 1
1. Evaluate 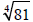
2. Evaluate 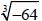
3. Evaluate 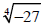
4. Evaluate 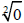
Square Roots and Cube Roots
1. The second root of a is called the square root of a.
i.e. 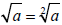 is read “the square root of a” is read “the square root of a”
2. The third root of a is called the cube root of a.
i.e. 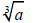 is read “the cube root of a” is read “the cube root of a”
Definition of 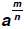
If 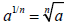 is a real number, then is a real number, then
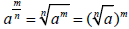
where
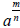 is the exponential
form of the expression, and is the exponential
form of the expression, and
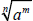 is the radical form of the
expression. is the radical form of the
expression.
Example 2
Put each expression in radical form.
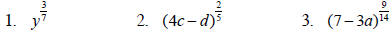
Example 3
Put each expression in exponential form.
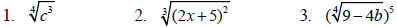
Example 4
Simplify each expression (reduce the index).
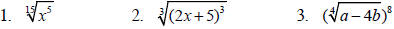
Product Property of Radicals
If 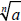 and and
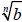 are real numbers, then are real numbers, then
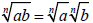
In words this tells us the nth root of the product
is the product of nth roots. In terms of the order
of operations, when the only operations are nth-rooting
and multiplying, then it does not matter
which operation comes first.
| Proof
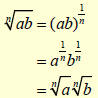 |
Condition #1 for a Simplified Radical Expression
A radical expression 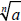 is not simplified when
the is not simplified when
the
radicand a has any perfect nth-power factors.
Example 1
Since n = 2, the radicand a can have no perfect square
factors.
Simplify 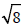
Simplify 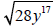
Example 2
Since n = 3, the radicand a can have no perfect cube
factors.
Simplify 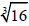
Simplify 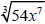
Example 3
Since n = 4, the radicand a can have no 4th-power factors.
Simplify 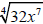
Simplify 
Example 4 Simplify each expression.
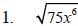
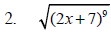
Example 5 Simplify each expression.
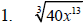
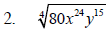
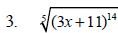
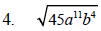
Condition #2 for a Simplified Radical Expression
The radical expression 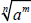 is not simplified if
m and n is not simplified if
m and n
have any common factors. That is, m/n must be in simplest
terms.
Example 6
Simplify each expression.
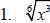
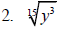
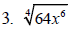
|