Radical Functions
 Section 3.4 Section 3.4
 Modeling continuous relationship which is Modeling continuous relationship which is
increasing and concave down
Model: Cost Function
 A company manufactures a A company manufactures a
quantity q of a product per month.
They invest $2.3 million in capital
towards technology (machinery,
computers, etc.) and a fixed cost
investment of $5.4 million. Data
is collected on the cost for varying
quantities q (in 100,000 units).
 Determine a model for cost. Determine a model for cost.
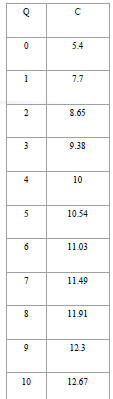
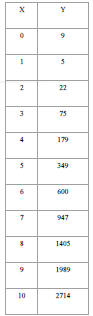
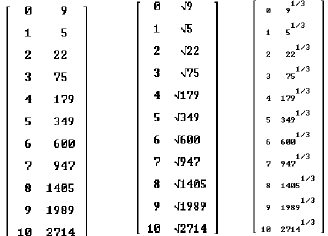
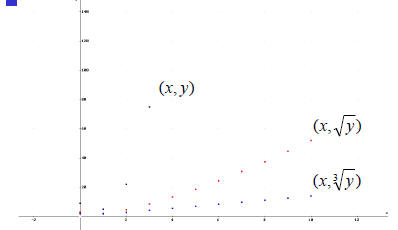
Cost Data
Properties of Model
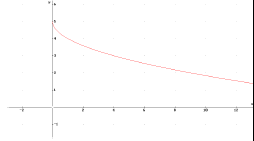
 Is the data increasing or decreasing? Is the data increasing or decreasing?
 Cost increases as production increases Cost increases as production increases
 Is the data concave up or concave down? Is the data concave up or concave down?
 Data is concave down Data is concave down
 Use the Ladder of Powers to determine a Use the Ladder of Powers to determine a
model with these characteristics. Can
it be a
polynomial model?
 No, polynomial functions are either increasing No, polynomial functions are either increasing
concave up or decreasing
concave down
Radical Functions
 Function of form Function of form 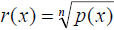
where p(x) is a polynomial, integer n>1
 If n is even, what is the domain of r(x)?
If n is even, what is the domain of r(x)?
 If n is odd, what is the domain of r(x)?
If n is odd, what is the domain of r(x)?
 What is the concavity of a radical power
What is the concavity of a radical power
function y = axn when 0 < n < 1?
Radical Function:
index 0<n<1
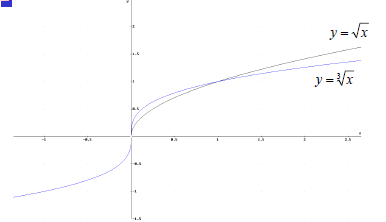
Determining Radical Model
 Ladder of Powers to decide if n = ½, Ladder of Powers to decide if n = ½,
n = 1/3, n = ¼ etc.
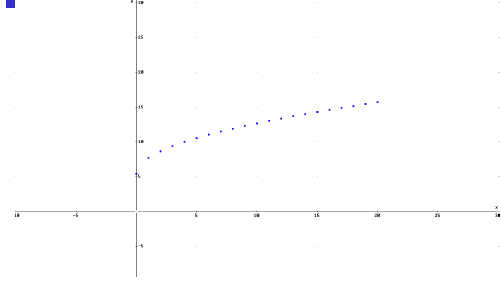
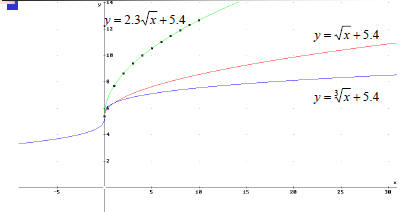
 Graph
Graph 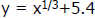 and and 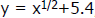 , which is , which is
a better fit to the Cost Data?
 Use Derive or a graphing calculator to fit a
Use Derive or a graphing calculator to fit a
radical function to the data
 Solution: Solution: 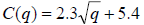
 Cobb-Douglas Production Function
Cobb-Douglas Production Function
Cost Model
Solving Radical Equations
-Algebraic Method
 Isolate the radical expression Isolate the radical expression
 Undo the nth root by using the inverse Undo the nth root by using the inverse
function –the nth power
 For which nth roots do we need to check for For which nth roots do we need to check for
extraneous roots?
 If nth root is even, taking an even power can If nth root is even, taking an even power can
result in extraneous roots
 If nth root is odd, taking an odd power will not If nth root is odd, taking an odd power will not
result in extraneous roots
Double Radical Equation
 Isolate one of the radical expressions Isolate one of the radical expressions
 Take the square to remove one of the square roots Take the square to remove one of the square roots
 Isolate the remaining radical and square again Isolate the remaining radical and square again
 Check for extraneous roots Check for extraneous roots
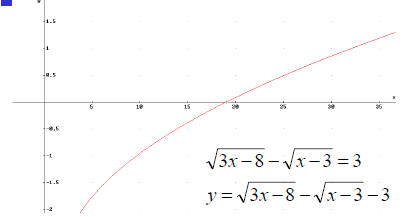
 Solve using algebraic and graphic method Solve using algebraic and graphic method
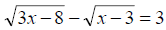
Double Radical Equation
Class Participation Exercise
1. Determine what
type of function
has the given
graph? Is it
polynomial or
radical? Why?
2. Solve the following radical equation:
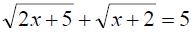
Linearization
 Use radical function to Use radical function to
make nonlinear polynomial
data linear
 Model the linear data Model the linear data
 Convert linear model into Convert linear model into
polynomial model
Linearization
 Use Derive or graphing calculator to Use Derive or graphing calculator to
plot data and transformed data
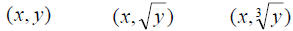
 Which of these makes the data linear? Which of these makes the data linear?
Linearization –Transformed Data
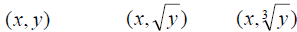
Linearization –Data Plot
Linearization
 Which transformed data is linear? Which transformed data is linear?
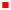 Solution: Cube root, so data is modeled by
Solution: Cube root, so data is modeled by
a cubic function
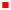 Linearized data model: y = 1.3x + 0.77
Linearized data model: y = 1.3x + 0.77
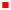 Actual data model: Actual data model:
 Best fit cubic model:
Best fit cubic model:
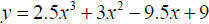
|