Multiplication of Radicals
In this section we want to learn how to multiply
expressions containing radicals.
First we will need to recall the following property from section 8.2
| Product Property of Radicals |
If 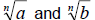 are real
numbers then,  |
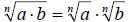For multiplying radicals we really want to look at this
property as 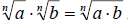 This means to multiply radicals,
we simply need to multiply the coefficients together and multiply the radicands
together. Then simplify as usual.
Example 1:
Multiply.
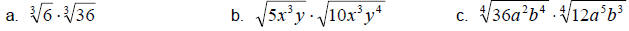
Solution:
a. Using the property above, we simply multiply the radicands together and then
simplify.
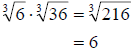
b. Just as above we multiply the radicands and simplify.
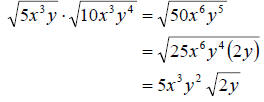
c. Again, we proceed as above.
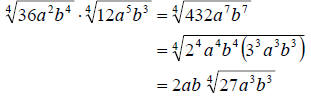
Now, in order to multiply expressions containing more that
one term, we will simply multiply as we did with polynomials in the past. That
is, we multiply each term in the first expression by each term in the second
expression, and simplify.
Example 2:
Multiply.
Solution:
a. Since we are to multiply as we did with polynomials, we need to use the
distrubutive property here. We must always keep in mind, though, that to
multiply radicals we multiply the radicands. So we get
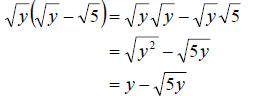
b. In this example we have to remember that we cannot pull
an exponent though a set of parenthesis if the operation inside is addition or
subtraction. Instead we need to write out binomial twice and then multiply out
as we did before. That is with either the FOIL method or multiplying each term
in the first expression by each term in the second. We get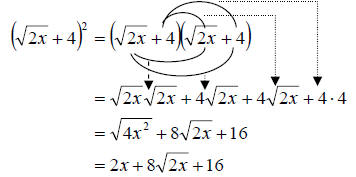
c. This time we simply proceed like we did in part b.
Multiply each term in the first by each term in the second. This gives
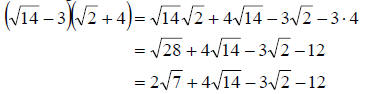
d. Again, proceed like we did above.
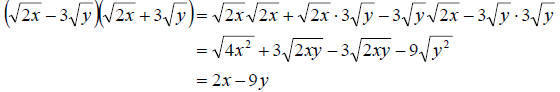
Notice in the very last example that the answer ended up
with no radicals. We call it a “radical free” expression. We also notice that
the two expressions 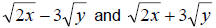 only differ by the sign
between the terms. When this is the case we call the expressions conjugates.
| Definition: Conjugates |
The expressions
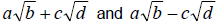 are called conjugates. Conjugates
always have a product that is “radical free”. |
We will need conjugates in an important way in the next
section. For now we simply need to remember that they always multiply to give an
expression containing no radicals.
8.4 Exercises
Multiply
|
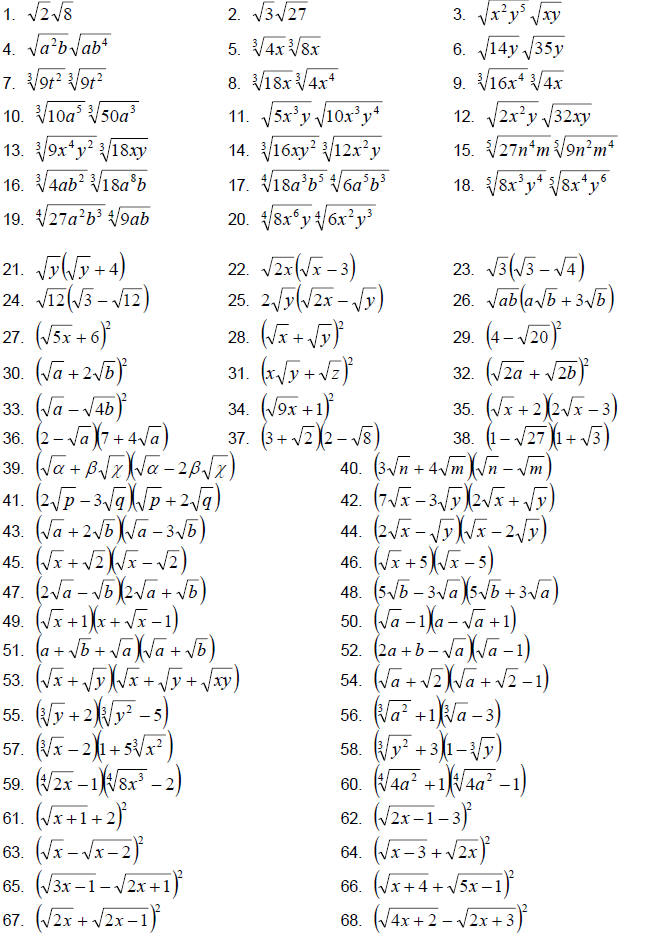
