Roots, Radicals, and Fractional Exponents
Radical notation
If we have something like
(1)
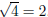 , ,
the symbol around the 4 is called a radical symbol, and in this case, it
indicates that we want the positive
square root of 4. That is, we want the positive number (or zero) that we can
raise to the power 2, and get 4.
Most numbers have two square roots, one positive and one negative. If we want
the negative square root,
we’ll put a negative sign out in front.
(2)
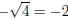 . .
Similarly,
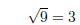
(3)
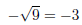
With only our normal real numbers, we can’t square a number (raise it to the
second power), and get a
negative number, so we don’t have any square roots for negative numbers.
(4)
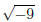 does not exist
does not exist
The square root symbol is actually a shorthand notation for
(5)
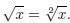
The little 2 with the radical symbol indicates that we want the inverse of the
x2 operation. By inverse, I
mean that we have
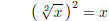 and
and
(6)
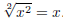
A square root followed by a square, or vice versa, gets us back to where we
started.
Similarly,
(7)
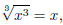
and the little 3 on the radical symbol indicates that we want the cube root or
the third root. This would be
the opposite of raising to the third power, and the cube root is the number we
would cube to get the number
inside. For example,
(8)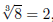
since 23 = 2 · 2 · 2 = 8. Since raising a negative number to the third power
gives us a negative number, it’s
possible to find a cube root of a negative number. For example,
(9)
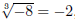 . .
since (−2)3 = (−2)(−2)(−2) = −8.
Quiz 25, Part I
Simplify the following.
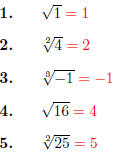
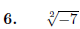 Does not exist
Does not exist
Fractional exponents
Recall that
(10)
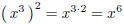 . .
When we raise an exponent expression to another exponent, we multiply the
exponents. If an exponent of
1/2 made sense, therefore, we should have
(11)
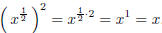 . .
This should look a lot like
(12)
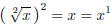 . .
Someone had the bright idea to define
(13)
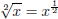 ,
,
and this ends up working really well.
All the roots work this way. For example,
(14)
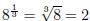 . .
You can even have things like
(15)
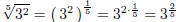 .
.
The bottom number in the fraction is always a root, and the top number is always
a regular power. With
all positive numbers, at least, the regular power can be on the inside or the
outside of the radical.
(16)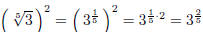 .
.
Quiz 25, Part II
Write using fractional exponents.
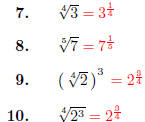
Write using radical notation.
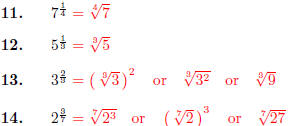
1. Using your calculator
In general, the expressions we’re looking at are not whole numbers, and for a
variety of reasons, we will
sometimes want to convert these to decimal form. It is relatively easy to do
this with our calculators once
we have the expressions written in terms of exponents.
Remember that your calculator has an exponent button. It
will probably have ^, xy, or yx on it. To check,
do the following computation.
(17) 32.
Your button sequence would have been something like: 3, ^, 2, =, and your answer
should be 9.
Your calculator also has a square-root button. It probably has a
 symbol on it.
Try the following symbol on it.
Try the following
computation to make sure you know how your calculator works.
(18) 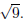
Some of you will key in: 9, 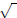 . Some of you will key in: . Some of you will key in:
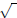 , 9. Make sure you
get 3 as your answer. , 9. Make sure you
get 3 as your answer.
You don’t really need a 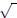 key, since you can use your exponent key. For example,
we know that key, since you can use your exponent key. For example,
we know that
(19) 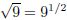 . .
The key sequence on your calculator will be: 9, ^, (, 1, ÷, 2, ), =. Note that
the 1÷2 is 1/2 , and this needed
to be in parentheses so that this is computed before doing the exponent.
Here’s another example. Compute
(20) 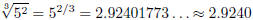
rounded to four decimal places. Your key sequence would be: 5, ^, (, 2, ÷, 3, ),
=.
Here are a few more rounded to four decimal places.
(21)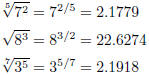
Quiz 25, Part III
Convert the following to decimal form, and round correctly to four decimal
places.
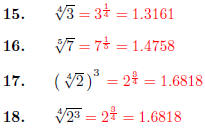

Homework 25
Convert the following to decimal form and round correctly to four decimal
places.
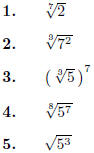
Write using radical notation.

|