Algebra
Tutorials!



	Home
	Exponents and Radicals
	Division of Radicals
	Exponents and Radicals
	RADICALS & RATIONAL EXPONENTS
	Radicals and Rational Exponents
	Radical Equations
	Solving Radical Equations
	Roots and Radicals
	RADICAL EQUATION
	Simplifying Radical Expressions
	Radical Expressions
	Solving Radical Equations
	Solving Radical Equations
	Exponents and Radicals
	Exponents and Radicals
	Roots;Rational Exponents;Radical Equations
	Solving and graphing radical equations
	Solving Radical Equations
	Radicals and Rational Exponents
	exponential_and_radical_properties
	Roots, Radicals, and Root Functions
	Multiplication of Radicals
	Solving Radical Equations
	Radical Expressions and Equations
	SOLVING RADICAL EQUATIONS
	Equations Containing Radicals and Complex Numbers
	Square Roots and Radicals
	Solving Radical Equations in One Variable Algebraically
	Polynomials and Radicals
	Roots,Radicals,and Fractional Exponents
	Adding, Subtracting, and Multiplying Radical Expressions
	Square Formula and Powers with Radicals
	Simplifying Radicals
	Exponents and Radicals Practice
	Solving Radical Equations
	Solving Radical Equations
	Solving Radical Equations
	Lecture-Radical Expressions
	Radical Functions

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Radical Equations

Student Learning
Outcome: To solve
radical equations using
the power rule.

Real-World Connection

• You can use radical
equations to solve
problems involving
oceanography and
recreation such as
designing an
amusement park.

DEFINITION

• Radical equation – an equation that has a
__________ in the radicand

• Example: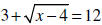

Connection

• We solve radical equations the __________ way
we’ve solved earlier equations: isolate the
variable, solve and check.

• Refresher:
Solve
3x + 4 = 2x – 6.
3x – 2x = -6 – 4
x = -10

Check:
3(-10) + 4 = 2(-10) – 6
-30 + 4 = -20 – 6
-26 = -26

Power Rule for Solving Radical
Equations, page 527

• If both sides of an equation are raised to the
same power, all solutions of the original
equation are also solutions of the new
equation.

• In other words, to “get rid of a radical”,
raise __________ sides to the same
__________ as the index.

Steps for
Solving Radical Equations

1. Isolate the __________. (Get it on one side
of the equation by itself.)

2. Use the power rule to __________ the
radical. (Raise both sides to the “root’s”
power.)

3. Solve.

4. Check. (Very important!)

Getting Started

• Solve each equation. Check your solution.

You try…

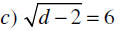
Definition

• Extraneous solution – a solution that does not
satisfy the __________ equation

Note: Extraneous solutions can occur when you
square both sides of an equation to create a
new equation. Always check your answers to
be sure none are “extraneous”.

• Special note: If all solutions are
extraneous, the equation has “no
solution”.

See Example 2, page 528.

More Examples

Even More…

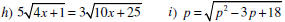
ASSIGNMENT

• My Math Lab

• Page 521, 1-73 odd, 77-81 odd

• Page 531, 1-25 odd