Exponential And Radical Properties
Exponential Properties:
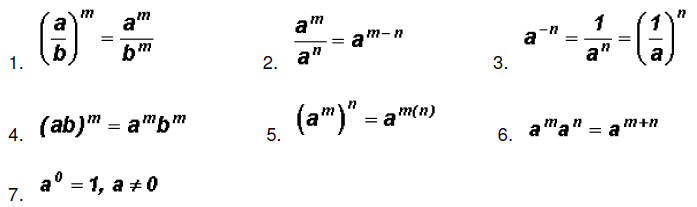
NOTE 1: There is no exponential rule for a sum or difference!
For example,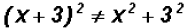 . .
Instead, you have to use FOIL. That is,
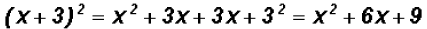
NOTE 2: Observe that 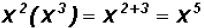 , but , but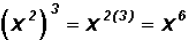 !
!
Radical Properties:
1. If 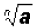 and and
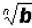 exist, then exist, then
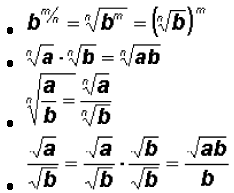
The denominator is usually rationalized!
2. For all real numbers a and n a positive integer:
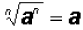 if n ≥ 3 is odd if n ≥ 3 is odd
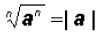 if n ≥ 2 is even if n ≥ 2 is even
3. If a is a positive real number,
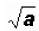 is the positive square root of a
is the positive square root of a
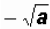 is the negative square root of a
is the negative square root of a
4. If a is a positive real number that is NOT a perfect
square, then
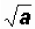 is irrational.
is irrational.
Any number that is the square of a rational number is called a perfect square.
For example, 144 is a perfect square (122 ) and
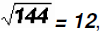 where 12 is a
where 12 is a
rational number.
However, 3 is NOT a perfect square and
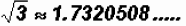 ,where ,where
1.7320508 ..... is an irrational number.
NOTE: A Rational Number can be written as a fraction
whereas an
Irrational Number cannot!
5. If a is a negative real number, then
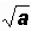 is an imaginary number.
is an imaginary number.
Example 1:
Write
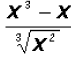 as a product and then simplify using the Distributive Property. Write your
answer
as a product and then simplify using the Distributive Property. Write your
answer
using rational exponents.
The Distributive Property states that if a(b + c), then we
can multiply a with each term in
parentheses, that is ab + ac.
The Distributive Property can also be extended to more
than two numbers, for example,
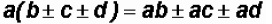
Note that in the case of, say, 2(x + 1)(x - 3) we can
apply the Distributive Property to
ONLY one of the binomials. We either distribute the 2 to (x + 1) OR to (x - 3).
That is, (2x + 2)(x - 3) OR (x + 1)(2x - 6), but NOT (2x + 2)(2x - 6).
First, we'll change the radical in the denominator to
rational exponent form.
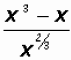
Now we'll write the expression as a product as follows:
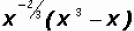
By the Distributive Property, we get
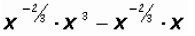
Then let's use Exponential Properties to simplify
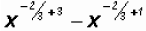
Since rational exponents are always written as improper
fractions and NOT as mixed
numbers, we'll need to find a common denominator. That is,
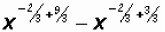
and finally, we get
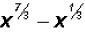
Example 2:
Let's use the expression from Example 1 again. But this
time, we carry out the division first and then
we simplify. Again we want to write the answer using rational exponents.
First, let's split the fraction and change the radical in the denominator to
rational exponent form
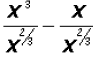
then let's use Exponential Properties to simplify
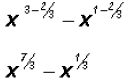
Example 3:
Combine like terms in
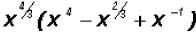 and write your answer using rational exponents.
and write your answer using rational exponents.
By the Distributive Property
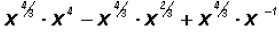
and using Exponential Properties we find
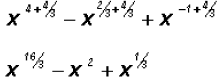
Example 4:
Rewrite the following exponential expressions as radicals
and simplify:
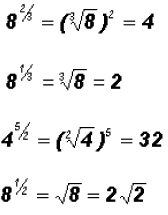
Example 5:
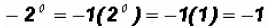
NOTE: By the Order of Operation, exponential expressions are simplified BEFORE
we multiply (in
this case by -1)!
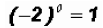
Example 6:
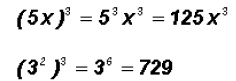
However,
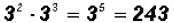
Example 7:
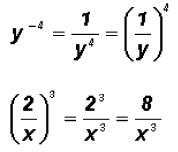
Example 8:
Rationalize the denominator
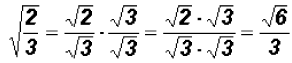
Example 9:
Find
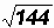 .
This radical represents the positive square root of 144. .
This radical represents the positive square root of 144.
Since 122 = 144 then
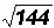 = 12
= 12
Please note that we DO NOT assume that is also equal to -12 !!! See Example
10!
Example 10:
Find
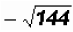 .
This radical represents the negative square root of 144. .
This radical represents the negative square root of 144.
Since (-12)2 = 144 then
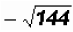 = -12
= -12
|