Equations Containing Radicals and Complex Numbers
PURPOSE
In this lesson you will continue to work with irrational numbers. You will
also be introduced to the
imaginary number system.
OBJECTIVES
After completing this lesson, you should be able to
•simplify products and quotients of binomials that contain radicals;
•solve equations involving radicals;
•find decimal representations of real numbers;
•use imaginary numbers to simplify radical expressions; and
•add, subtract, multiply, and divide complex numbers.
READING ASSIGNMENT
Chapter 6, Sections 6–4 through 6–8
COMMENTARY
Section 6–4: Binomials Containing Radicals (pages
274–275)
When multiplying an expression that contains a radical by
another expression that contains a radical,
you must multiply radicals by radicals and nonradicals by nonradicals. The
radicals do not have to
be like radicals to multiply.
Example 1: Simplify
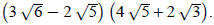
The multiplication is done as with multiplying binomials:
First, Outer, Inner, Last (FOIL):
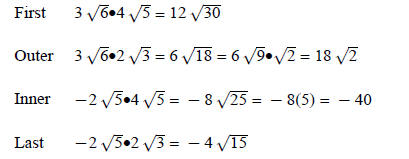
Add values together:
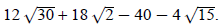
Because none of the terms have like radicals, this is the
simplified answer.
Example 2: Simplify
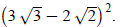
Remember when a quantity is involved, you multiply the
quantity by itself; you do not square the
individual terms. Try this and then check your simplification:
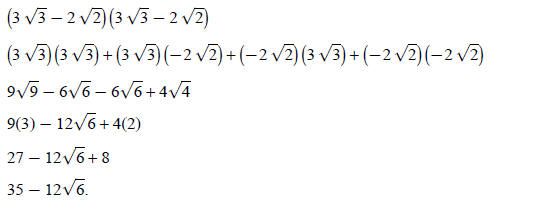
Rationalizing a denominator that contains a binomial is a
little different than when the denominator
is not a binomial. Let's experiment with the fraction
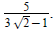
If the denominator were only 3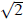 ,
then you would multiply ,
then you would multiply 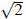 by the numerator and
denominator: by the numerator and
denominator:
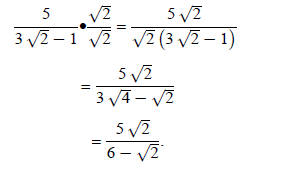
Notice the denominator still has a radical in it. The
denominator has not been rationalized.
If we multiply the denominator by the same binomial but
change the middle sign, the radical will fall
out. That denominator is called the conjugate of the denominator:
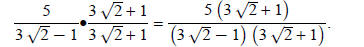
The radicals are opposite so they subtract out:
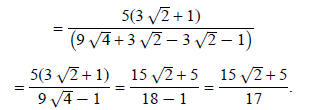
Example 3: Simplify
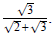
Try this yourself and check your simplification:
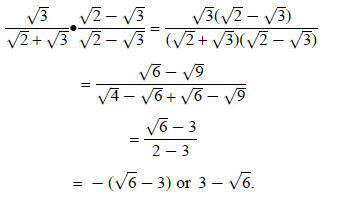
Example 4: Simplify
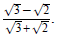
Try this yourself and check your simplification:
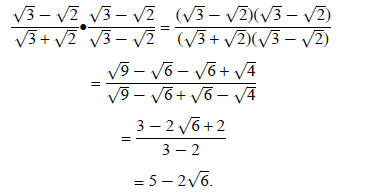
Example 5: Find
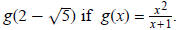
The domain of the function is
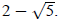 Place Place 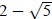 in
for the x variables in the function so that in
for the x variables in the function so that 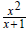
becomes 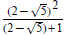 and, then, simplify: and, then, simplify:
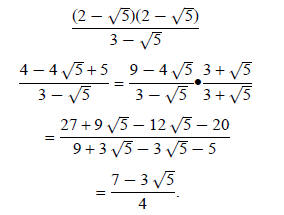
Example 6: Show by substitution that
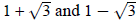 are roots of x^2 − 2 x − 2 = 0. are roots of x^2 − 2 x − 2 = 0.
Substitution requires placing the roots in for x. Then do
the math to show the equation equals zero.
Place the roots in one at a time. I will work through with the root
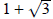 first. Then you can work first. Then you can work
through with the root 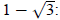
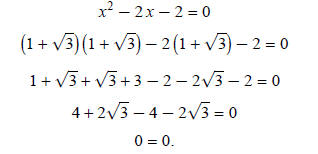
Your turn. If you have problems, check my figures below:
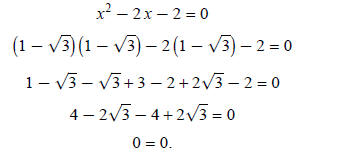
Example 7: For our last problem in this section,
let's simplify problem 44 on page 276 of your
textbook:
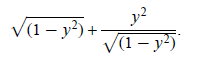
This problem is different because the denominator of the
second term has the subtraction problem
within the radical. This means you do not use the conjugate. The conjugate is
used only when the
addition or subtraction sign is outside of the radical. Rationalize the
denominator by multiplying by
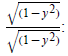
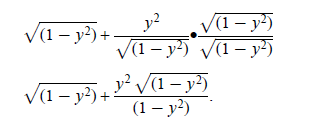
Now get similiar denominators:
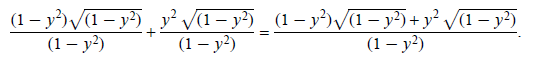
Use the distributive property:
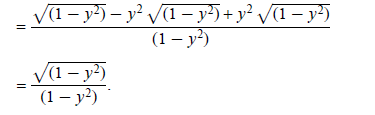
Study Exercises
Complete the odd–numbered problems 1–43 on pages 275–276
of the textbook. Check your answers
in the back of the textbook.
Section 6–5: Equations Containing Radicals (pages
277–279)
What is the difference between the equations
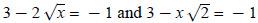 ? One is a radical ? One is a radical
equation, and one is not. A radical equation has the variable within the
radical. Squaring is part of
the process of solving the radical equation. If the variable is not within the
radical, squaring is not
part of solving the equation. The key to solving radical equations is to get the
radical term on one
side of the equation by itself. After the radical term is alone, you can raise
both sides to the power
that will be the inverse operation of the radical. The radical is then gone and
the equation can be
solved. Sometimes when solving a radical equation, an extraneous root may be
found. This is a root
that is not a solution. For this reason, you must check all roots in the
original equation to be sure the
root found is a true solution. Both equations are solved below:
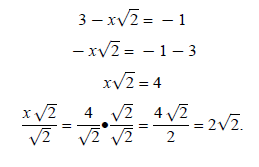
This does not have to be checked because the equation was
not a radical equation. The variable was
not in the radical:
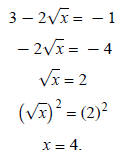
This does need to be checked, because the original
equation was a radical equation:
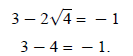
4 is a solution.
Example 1: Solve
Work to get the radical term,
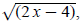 alone. This will require adding the 2 over: alone. This will require adding the 2 over:
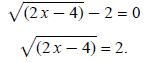
The radical term is now alone. The radical term uses the
square root. So square both sides of the
equation:
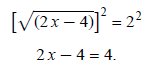
Continue to solve:
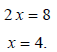
Now check the root to make sure it is not an extraneous
root:
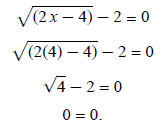
The solution is 4.
Example 2: Solve
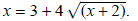
Begin by isolating the radical term:
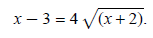
Square both sides:
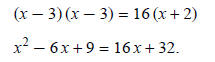
Move all terms to one side, set equal to zero:
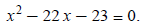
Factor:
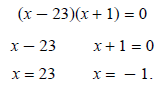
Now check the solutions. Double-check yours against mine.
The only solution is 23:
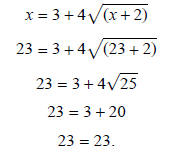
−1 is an extraneous root:
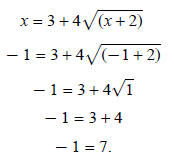
Example 3: Solve
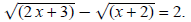
In this problem, you cannot isolate the radical term.
There are too many of them. But the problem
can be made easier by separating the radical terms:
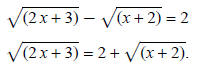
Square both sides:
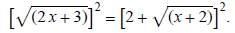
Notice the right side must be squared as a quantity:
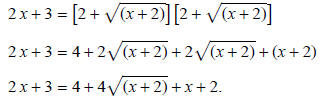
Again work to isolate the remaining radical:
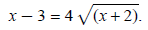
Square both sides again:
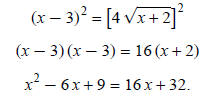
Move all terms to one side and set equal to zero:
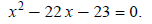
Factor:
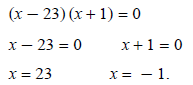
Now check the solutions. Double-check yours with mine.
The only solution is 23:
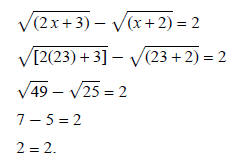
−1 is an extraneous root:
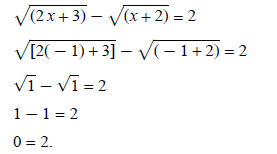
Example 4: Solve 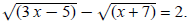 Then, solve and check.
Then, solve and check.
Separate radicals:
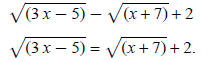
Square both sides:
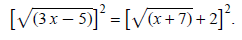
Square right side as a binomial:
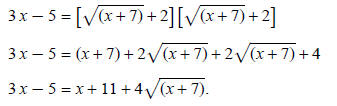
Work to isolate radical:
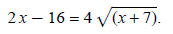
Square both sides:
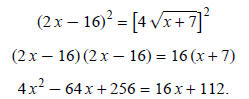
Move all terms to one side and set equal to zero:
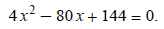
Factor:
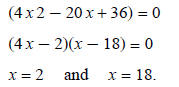
Check results:
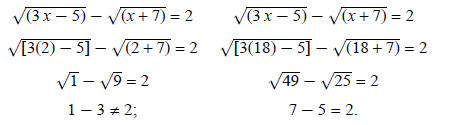
2 is an extraneous root. The only solution is 18.
Study Exercises
Complete the odd–numbered problems 1–35 on pages 280–281
and the mixed–review problems
1–11 on page 282 of your textbook. Check your answers in the back of the
textbook.
Section 6–6: Rational and Irrational Numbers (pages
283–285)
Lesson 1 introduced you to rational and irrational
numbers. A rational number may or may not
contain a decimal portion. If the number has digits to the right of the decimal,
the decimal portion
will eventually terminate, or the pattern of the digits will repeat. 3.4567 and
3.446544654465 are
both rational numbers.
An irrational number always has a decimal portion, and the
digits after the decimal will never repeat
or terminate. Irrational numbers always result when you take a root of a number
that is not a perfect
square or cube, etc. Pi is also an irrational number. In this section, you will
determine whether a
value is rational or irrational. You will also convert rational numbers from
fractions to decimals and
from decimals to fractions. To convert a fraction to a decimal, just divide the
numerator by the
denominator. To convert a decimal to a fraction, write the decimal the way you
read the fraction. For
example, the decimal 0.037 is read as "thirty-seven thousands," so write the
fraction as 37/1000. Finally,
reduce the fraction, if necessary. Converting repeating decimals to fractions
takes more skill.
Example 1: Convert
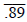 to a decimal. to a decimal.
The decimal repeats the pattern 89 endlessly. Because two
numbers are repeated, we will multiply
the decimal by 100, which contains two zeros. N will represent the fraction for
which we are
looking.
Subtract the two values and all of the repeating 89s will
subtract out:
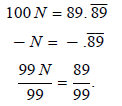
The fraction for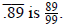 You
can divide 89 by 99 and see whether its decimal is the repeating You
can divide 89 by 99 and see whether its decimal is the repeating
decimal.
Example 2: Convert
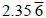 to a fraction. to a fraction.
Separate the number into its whole part and decimal part.
Use only the decimal part for the
conversion. Tack the 2 onto the fraction when finished. One digit repeats, so
multiply by 10, which
has one zero. Try this yourself and check your results:
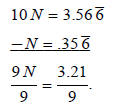
This is the fraction, but it contains a decimal. Multiply
the numerator and denominator by 100 to
move the decimal two places to the right: 321/900 simplifies to 107/300.
Tack on the 2 (from the original problem), and you have
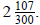
Study Exercises
Complete the odd–numbered problems 1–31 on page 286 of the
textbook. Check your answers in the
back of the textbook.
Section 6–7: The Imaginary Number i (pages 288–289)
After reading the pages in your textbook on the imaginary
number i, you realize that 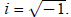 There There
are just a few things to remember when working with imaginary numbers:
1. The value of i^2 is −1. Because
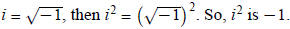
2. Always bring the i out of a radical before doing any
other simplification.
Example 1: Simplify
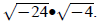
The incorrect method would be to multiply first:
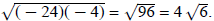 The i was lost The i was lost
because multiplication of two negative numbers results in a positive.
The correct method would be to bring the i out first:
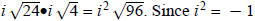 , the final , the final
simplification is 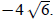 You will obtain a
different answer when you perform the simplification You will obtain a
different answer when you perform the simplification
correctly.
Example 2: Simplify
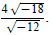
Before reducing the fraction, bring out the i:
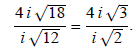
The value of i is 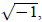 so i
is a radical. It cannot be left in the denominator: so i
is a radical. It cannot be left in the denominator:
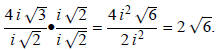
Example 3: Simplify
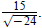
Try this yourself and then check it:
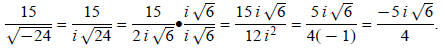
Example 4: Solve 5x^2 + 13 = 1:
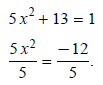
Next, take the square root of both sides. Remember that
the answer can be positive or negative when
taking the square root. Place the ± signs on the radical immediately. The ±
signs will stay out in
front of any other values brought out of the radical:
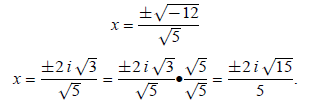
Example 5: Simplify
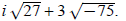
Begin by simplifying each radical:
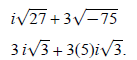
Add like terms:
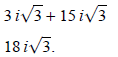
This section is a great review of radical work with a
slight twist involving i. Enjoy it!
Study Exercises
Complete the odd–numbered problems 1–53 ("Written
Exercises") on pages 290–291 of the
textbook and the odd mixed–review problems 1–13 on page 291. Check your answers
in the back of
the textbook. Section 6–8: The Complex Numbers (pages 292–294)
Complex numbers contain real and imaginary numbers.
Simplify these problems just as you have
been doing—just remember to treat i with respect!
Example 1: Simplify (13 − 4 i) − (3 i − 25):
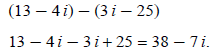
Example 2: Simplify (−3 + 4 i) (2 − 3 i):
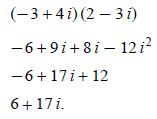
Example 3: Simplify (3 − 4 i)^2 (3 + 4 i)^2:
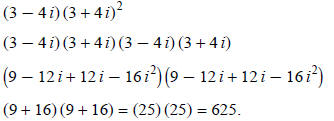
Example 4: Simplify
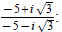
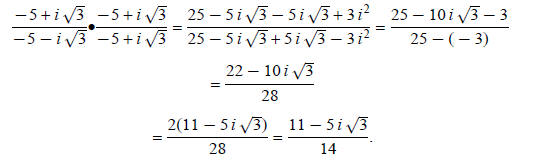
Example 5: Find the reciprocal of
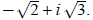
The reciprocal of 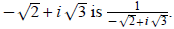 Now
rationalize the denominator: Now
rationalize the denominator:
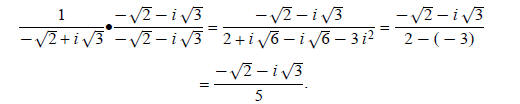
Example 6: If 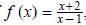 find
find 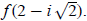
Place 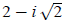 in for x. in for x.
Then check your simplification and answer:
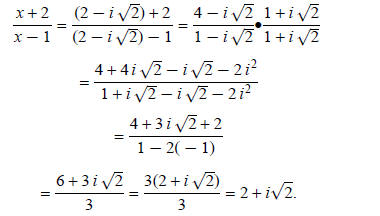
Study Exercises
Complete the odd-numbered problems 1–49 on pages 295–296
of the textbook. Check your answers
in the back of the textbook.
Now you are almost ready for your tenth and last progress
evaluation. There are self-tests on pages
282 (problems 11 and 13) and 297 of your textbook. You can also review odd
problems 7–15 on the
Chapter Review on page 302. The answers to these problems are located in the
back of your
textbook. You can also take the following quiz to help you prepare (answers are
at the end of this
lesson).
Quiz: Equations Containing Radicals and Complex Numbers
1. Simplify 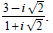
2. Simplify 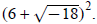
3. Give the fraction for
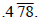
4. Solve 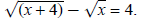
5. Solve 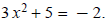
Answers
This section provides answers to the quiz in Lesson 10.
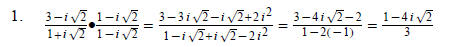
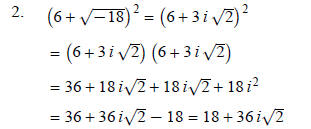
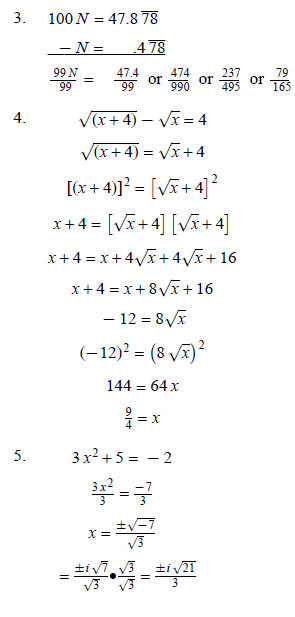
|