Solving Radical Equations
In this section we want to learn how to solve equations
containing radicals, like 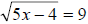 . In . In
order to do this we need the following property.
| n-th Power Property |
If 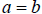 , then , then
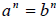 |
Basically, this property tells us we can raise both sides
of any equation to any power we would
like. However, we must be careful. There are several places where we can make
serious
mistakes.
First, we need to make sure that we really are raising the entire side to the
nth power and not just
each term individually. Also, when using the nth power property there is the
possibility that we
end up with solutions that don’t check, called extraneous solutions. The reason
we get these on
occasion has to do with the logical construction of the property. The property
tells us that if
something is a solution to 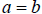 then it must also
be a solution to then it must also
be a solution to
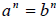 . That doesn’t mean . That doesn’t mean
that if something is a solution to
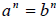 that it is a solution to that it is a solution to 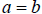 .
To rectify this, we simply .
To rectify this, we simply
check our answers and throw away the ones that do not work.
So, always remember, be careful to raise the entire side to the n-th power, and
we must always
check our answers.
Example 1:
Solve.
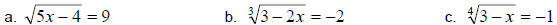
Solution:
a. We can use the n-th power property to get rid of the radical. Since we have a
square
root, we should use the second power, i.e. we should square both sides of the
equation.
Then we can solve like usual. We get
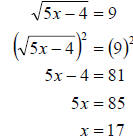
Now we must check our answer. We do this in the original
equation. If the value does
not check, then we eliminate it and would have no solution. We get
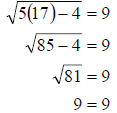
Since the value checks, our solution is set {17}.
b. Again, we need to raise both sides of the equation to a suitable power to get
rid of the
radical. This time we will use the 3rd power since we have a cube root. We get
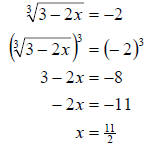
Now we check the solution.
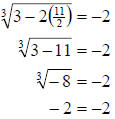
Since the value checks the solution set is
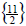 . .
c. Finally, we need to raise both sides to the 4th power since we have a 4th
root. We get
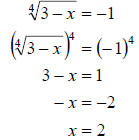
Check:
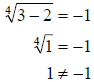
Since it does not check, 2 can not be a solution to the
equation. Therefore, we have the
equation has no solution.
Now, sometimes the equation is a bit more complicated. What we need to know is
that before
raising both sides to the n-th power, we must always isolate the
radical expression first. That way
we are assured that it will cancel when we
use the exponent. Also, sometimes, after raising both
sides to the n-th power,
we end up with a radical still in the equation. In this situation, we need to
again isolate the radical and again use the exponent. We keep repeating this
process until all the
radicals are gone. Then we solve as usual.
Example 2:
Solve.
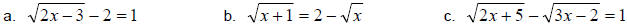
Solution:
a. First thing we need to do is isolate the radical. Once we have done that we
can square
both sides of the equation as we did in example1. Then, of course, we
finish solving and
check.
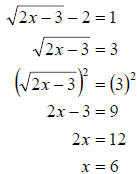
Check:
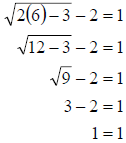
The value checks. Therefore the solution set is {6}.
b. Notice this time that one of the radicals is already isolated. Therefore we
can go ahead
and square both sides. Must, however be very careful with squaring
the right side since it
has two terms. It generally makes it easier to square
properly by writing the entire side
out twice and then multiplying as we learned
in section 8.4. We get
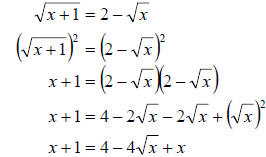
Notice that we are left with another equation that has a
radical. Therefore, we need to
isolate again and square again. In this case
however, it is easier to simply isolate the
term containing the radical and the
carefully square both sides. We can then continue
solving as usual.
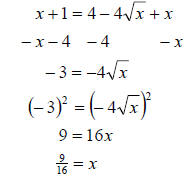
Check:
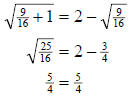
Since the solution checks, the solution set is
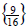 . .
c. Finally, we must start by isolating one of the two radicals in this equation.
We will choose
to isolate the positve one. Generally we isolate the more
complicated radical in order to
eliminate it first. However, either could be
isolated and still produce the correct solutions.
Once we have isolated the
radical then we can square both sides very carefully and then
continue as usual.
We get
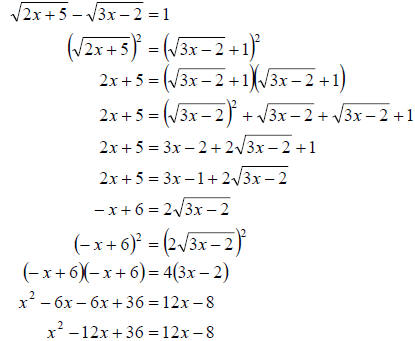
Recall, to solve an equation that has a squared term we
must solve by factoring. That is,
we get all terms on one side, factor and set
each factor to zero. This gives
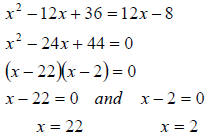
Now we must check both answers and keep only those which
work
Check:
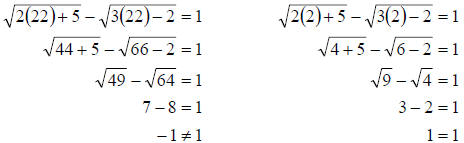
So, 22 does not check but 2 does. Therefore, the 22 is an
extraneous solution. So our
solution set is {2 }.
Finally we want to see some applications of radicals. The
first of these requires the Pythagorean
theorem. We state it below.
|