Solving Radical Equations
Now that we have learned how to work with radical
expressions we will move on to
solving. We must use caution when solving radical equations because the
following steps
may lead to extraneous solutions, solutions that do not solve the
original equation.
Whenever we raise both sides of an equation to an even
power we introduce the
possibility of extraneous solutions so the check is essential here.
A. Solve
The root determines what power to raise both sides to. For
example, if we have a cubed
root we must raise both sides to the 3rd power. The property that we are using
is
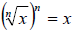for integers n > 1 and positive real numbers x. After eliminating the radical,
we will most likely be left with either a linear or quadratic equation to solve.
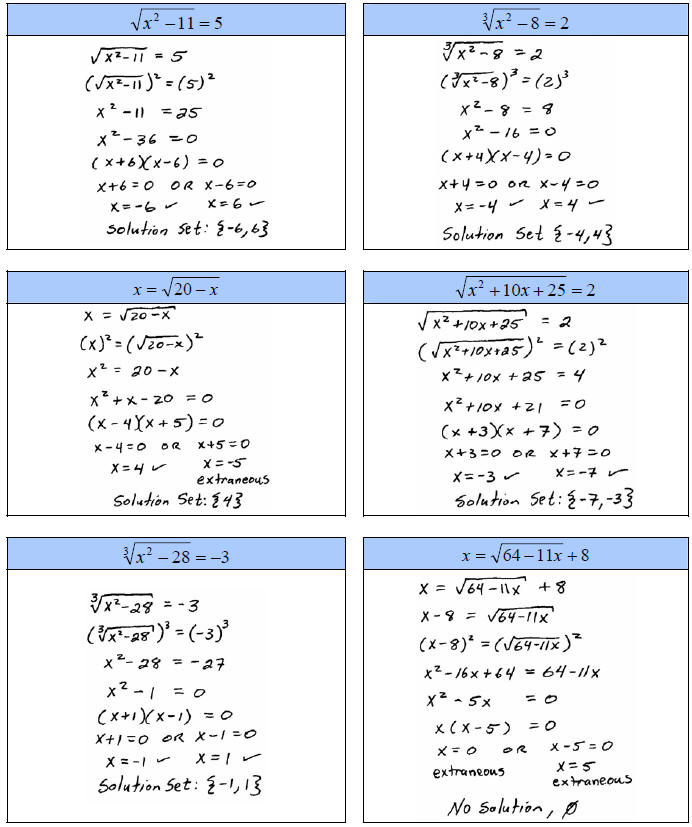
The check mark indicates that we have actually checked
that the value is a solution to the
equation, do not dismiss this step, it is essential.
The next set of problems is actually my personal favorite
because I grew up in Southern
California and I like to call them “totally” radical equations!
B. Solve
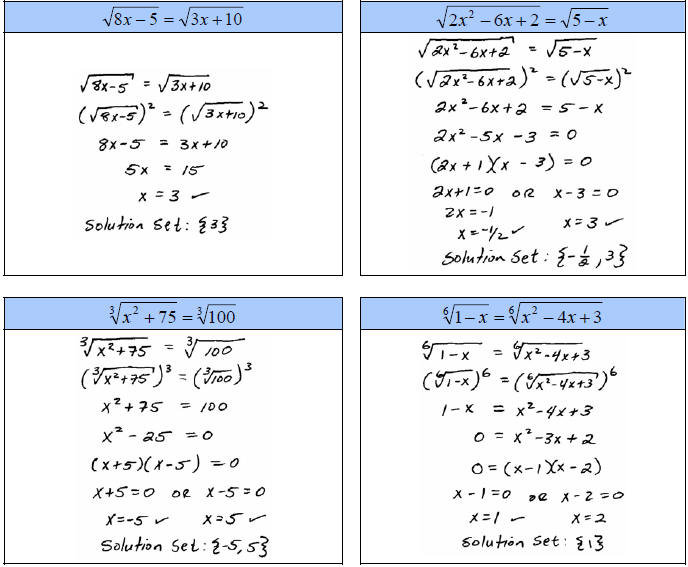
Students often have difficulty with radical expressions
where we have more than one
radical expression. These require us to isolate each remaining radical
expression and
raise both sides to the nth power until they are all eliminated. Be patient with
these, go
slow and avoid short cuts.
Tip: Use the formulas to save a step when squaring
binomials.
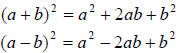
In the last problem, notice that I used the formula to
square the following binomial.
|
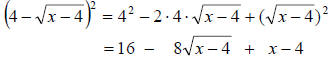
