RADICALS & RATIONAL EXPONENTS
Facts about Power Equations
Consider the power equation
xN = #,
with N > 1 integer and # any real number. Regarding the
solvability of
this equation, one has the following cases
I. If N is odd, the equation has one real solution, no matter what the
value of # is.
II. If N is even, then
(a) if # = 0 : the equation has one real solution x = 0;
(b) if # > 0 : the equation has two real solutions;
(c) if # < 0 : the equation has no real solutions.
EXAMPLE 1: The table below contains several equations, their solutions,
and the applicable cases
| Equation |
Solution(s) |
Case |
| x3 = 27 |
x = 3 |
I |
| x5 = −32 |
x = −2 |
I |
| x2 = 0 |
x = 0 |
II (a) |
| x2 = 144 |
x = 12, −12 |
II (b) |
| x4 = 625 |
x = 5, −5 |
II (b) |
| x2 = −4 |
no real sol. |
II (c) |
Radical Notation
With N and # as above, the notation
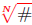
designates one special solution of the power equation xN =
#, namely:
I. If N is odd, the unique solution is chosen
II. If N is even, the non-negative solution is chosen.
This is applica-
ble only when # ≥ 0. In the case when # < 0, the radical 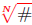 is is
undefined.
Convention: When N = 2, the radical 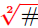 is
simply denoted by is
simply denoted by 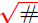
Based on the discussion on the equations in Example
1, we have:
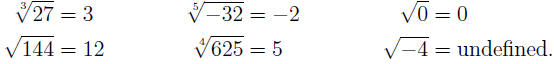
Properties of Radicals
| Undoing Formulas for Radicals.
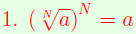
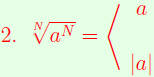 |
if N is odd |
| if N is even |
|
(UFR) |
| Arithmetic Formulas for Radicals.
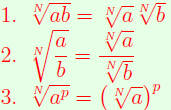
(Assuming N√a and N√b are defined.) |
(AFR) |
WARNING! What is incorrect about the equality
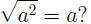
The above equality holds only when a ≥ 0. For instance, if
we try a = −12,
we have
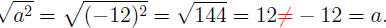
By (UFR2) we know that 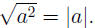
TIP: The above formulas can be used when we want to simplify
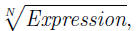
where Expression involves powers, products and quotients.
We do so by
• factoring N-powers out of Expression,
• then pulling N-powers outside 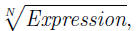 using (UFR)
and (AFR). using (UFR)
and (AFR).
EXAMPLE 2: Suppose we want to simplify
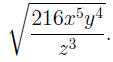
Using the equalities 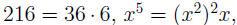 and
and 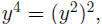 we see that we we see that we
can factor the square 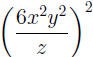 under the radical, then
we pull it out: under the radical, then
we pull it out:
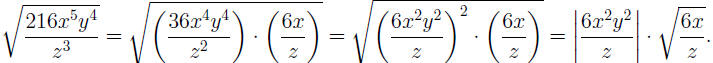
NOTE: Since N = 2 is even, we pulled out the square using
the absolute
value. If all variables x, y, z are assumed to be positive, the above simplifi-
cation can be continued (with last equality optional) as:
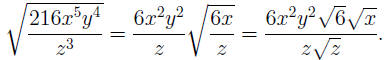
Fractions with radicals
Suppose we have a fraction, such as the one in Examples 3 and 4 below,
and we are asked to transform it (by multiplying both sides by the same
Expression) into an equivalent one
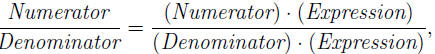
so that the new fraction is ”nicer.” The specification of
what ”nicer” means
is often formulated as a request:
• rationalize the denominator, or
• rationalize the numerator.
This means that we look for and expression, such that one of the products
(Numerator) ·(Expression) or (Denominator)· (Expression) is without radicals.
EXAMPLE 3: If we want to rationalize the denominator in
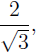 the expres- the expres-
sion is pretty obvious: (using 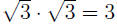 ): ):
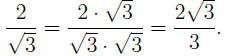
TIPS: For more complicated Numerators or Denominators, try
one of these
identities (based on (a + b)(a − b) = a2 − b2):
| Rationalizing tricks.
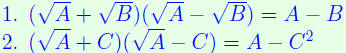 |
(RT) |
EXAMPLE 4: To rationalize the denominator in
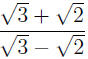
we multiply both sides by
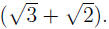 . Note that in the new numerator we . Note that in the new numerator we
have a square, for which we employ the Square of a Sum Formula ((a+b)2 =
a2 + 2ab + b2):
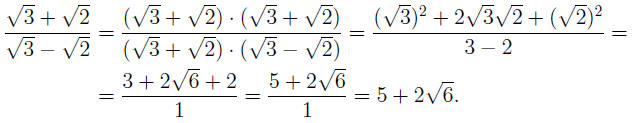
Fractional Powers (Rational Exponents)
Suppose 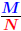 is a rational number (with the
fraction simplified). The is a rational number (with the
fraction simplified). The 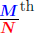
powers are computed using one of the equalities:
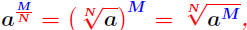 provided provided
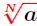 is defined is defined
In particular, for an integer N > 1, the
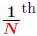 powers are computed by powers are computed by
 provided provided
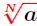 is defined is defined
EXAMPLE 5: To compute 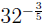 we use the definition with M = −3 and we use the definition with M = −3 and
N = 5, combined with (UFR2) and the equality 32 = 25:
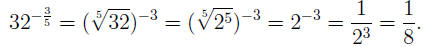
EXAMPLE 6: To convert 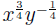 to radical notation, we use the second equal-
to radical notation, we use the second equal-
ity in the definition (for 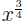 we use M = 3, N =
4; for we use M = 3, N =
4; for 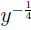 we use M = −1, we use M = −1,
N = 4), then we simplify (last equality optional) using (AFR1):
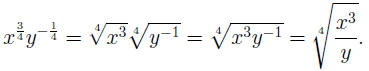
Arithemtic of Fractional Powers
FACT: The formulas first introduced in R2, collected in the table below, also
work if the epxonents m and m are rational.
| Arithmetic Formulas for Powers.
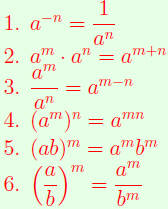
(Provided all powers are defined.) |
(AFP) |
EXAMPLE 7: To simplify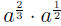 we add the exponents using (AFP1):
we add the exponents using (AFP1):
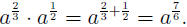
(How did we get 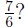 When
adding When
adding 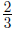 and and
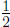 we converted them to fractions we converted them to fractions
with denominator 6, that is: 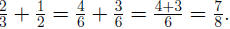 ) )
EXAMPLE 8: To convert 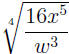 to rational exponents, we replace directly
to rational exponents, we replace directly
the 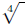 operation with the operation with the
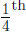 power, then (note that 16 = 24) we use (AFP): power, then (note that 16 = 24) we use (AFP):
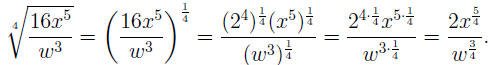
EXAMPLE 9: To convert 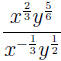 to
radical notation, we first simplfy (see to
radical notation, we first simplfy (see
also R2 for the technique of handling products and quotients of powers) the
expression using (AFP), then convert the factors to radicals :
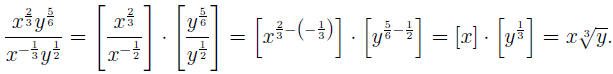
(Make sure you understand the calculations of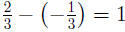 and
and 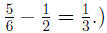
|