Exponents and Radicals
Combining Radical Expressions
Radical expressions can only be combined if there are like terms-terms with
the same index and same radicand
(the expression inside the radical).
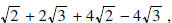
In the above expression, the terms with
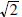 are alike and the terms with are alike and the terms with
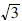 are alike. Therefore, the above are alike. Therefore, the above
expressions simplifies as follows:
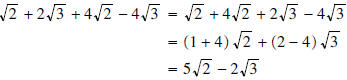
Notice that the two remaining terms are not alike and,
hence, cannot be simplified.
Some terms which do not look alike at first glance may be
alike after simplifying. Therefore, it is important
that you simplify all radicals before combining like terms.
Examples:
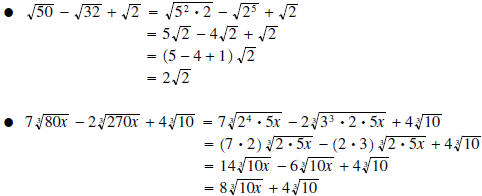
(note that these terms are NOT alike even though they both have a 10)
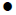 In simplifying In simplifying
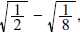 we begin by using Property we begin by using Property
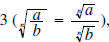 then simplifying and then simplifying and
rationalizing the denominator before combining:
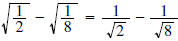 (Note that 8 = 4 • 2) (Note that 8 = 4 • 2)
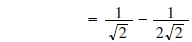 (Multiply both by (Multiply both by
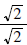 ) )
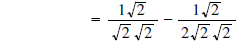
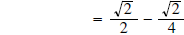 (now get a common denominator) (now get a common denominator)
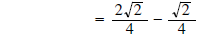
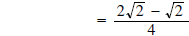 (now combine radicals) (now combine radicals)

|