Radical Expressions and Equations
As long as the roots are the same we can multiply the
radicands together using the following property.
Multiplying Radicals – Given positive real numbers
A and B and integer n > 1:
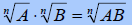
Since multiplication is commutative just multiply the
coefficients together and multiply the radicands together, if the roots are the
same, then simplify.
A. Multiply

Take care to be sure that the roots are the same before
multiplying. We will assume that all variables are positive.
B. Simplify


When dividing radical expressions, as long as the roots
are the same, we can divide the radicands using the following property.
Dividing Radicals – Given positive real numbers A
and B and integer n > 1:
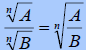
It is our choice to divide the radicands first or simplify
first then divide. Either way we choose to work the following problems the
results will be the same.
C. Divide (assume all variables are positive)

Rationalizing the Denominator
A simplified radical expression can not have a radical in
the denominator. When the denominator has a radical in it we must multiply the
entire expression by some form of 1 to eliminate it. The basic steps follow.
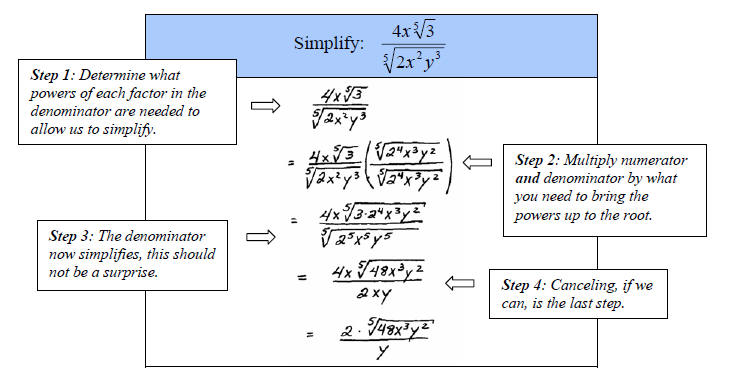
D. Rationalize the denominator.

Tip: When rationalizing the denominator the root
drives our choices. Multiply numerator and denominator by what you need to raise
all the powers of the denominator to equal the root.
This technique does not work when dividing by a binomial
which contains a radical. A new technique is introduced to deal with this
situation.
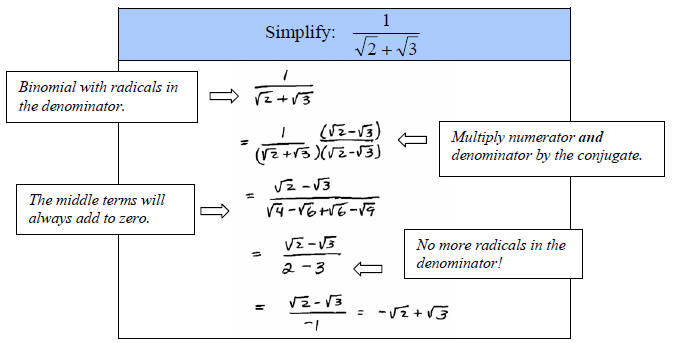
If we have a radical expression of the form
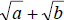 then its conjugate is then its conjugate is
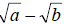 and and
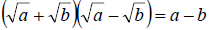
E. Rationalize the denominator.

|