Square Formula and Powers with Radicals

A. Square Formula

Recall the square formula:

Square formula:

1.Square the first term

2.Product times two

3.Square the last term

After applying the square formula with radicals, remember to simplify.

B. Examples

Example 1: Simplify

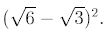
Solution

Apply the square formula:

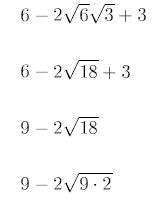
Thus we get

Ans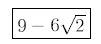

Example 2: Simplify

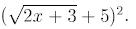
Solution

By the square formula, we have

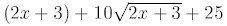
Combining like terms, we have

Ans

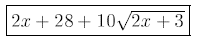
Example 3: Simplify

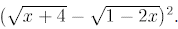
Solution

By the square formula, we have

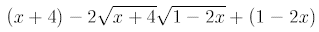
Combining like terms, we have

Ans

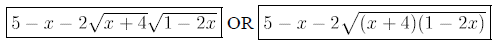
Example 4: Simplify

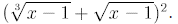
Solution

By the square formula, we have

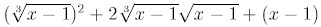
Bringing the power to the inside and rearranging, we have

Ans

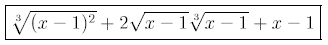
C. Powers

Recall that we use the square formula repeatedly with FOIL/factor table.

Example 1: Simplify

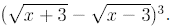
Solution

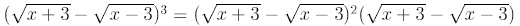
Now apply the square formula:

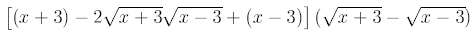
Combining like terms:

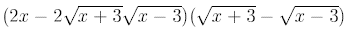
Now use FOIL to get the answer:

Ans

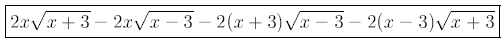
Example 2: Simplify

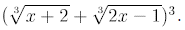
Solution

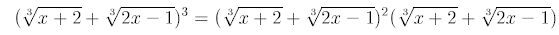
Now apply the square formula:

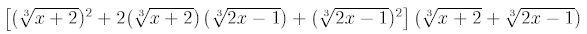
Use the factor table:

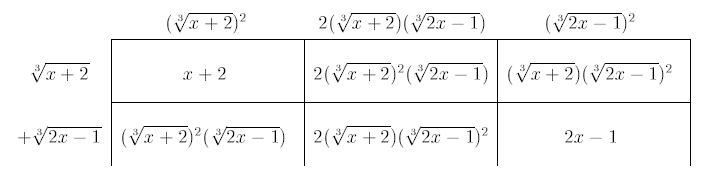
Thus we have

Ans
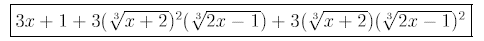